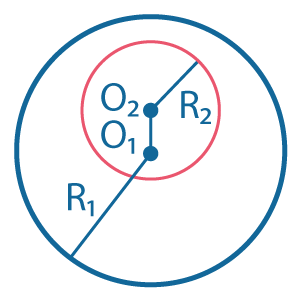
Одна окружность касается другой изнутри - окружности имеют одну общую точку \(M\), лежащую на прямой \(O_1O_2\).
Одна общая касательная \(a\) проходит через эту точку и перпендикулярна прямой \(O_1O_2\).
Расстояние между центрами окружностей равно разности их радиусов: \(O_1O_2=R_1-R_2.\)

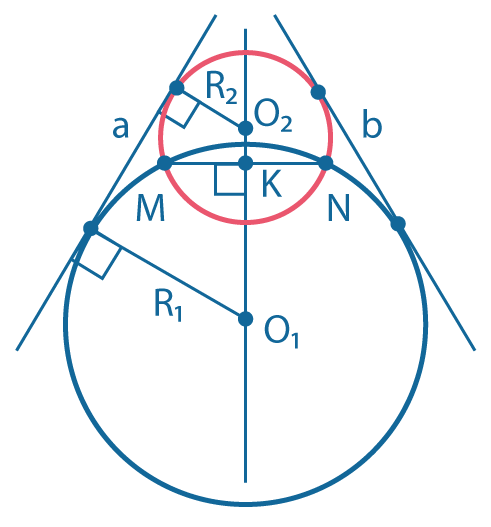Окружности пересекаются - имеют две общих точки \(M\) и \(N\).
Если две общих кастаельных \(a\) и \(b\). Если радиусы окружностей равны, то касательные параллельны, а если радиусы не равны, то касательные пересекаются в точке, лежащей на прямой \(O_1O_2\).
Общая хорда \(MN\) перпендикулярна прямой \(O_1O_2\) и делится ею пополам: \(MN\perp O_1O_2;~ MK=KN\).
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы:

\(R_1-R_2 < O_1O_2 < R_1+R_2\)

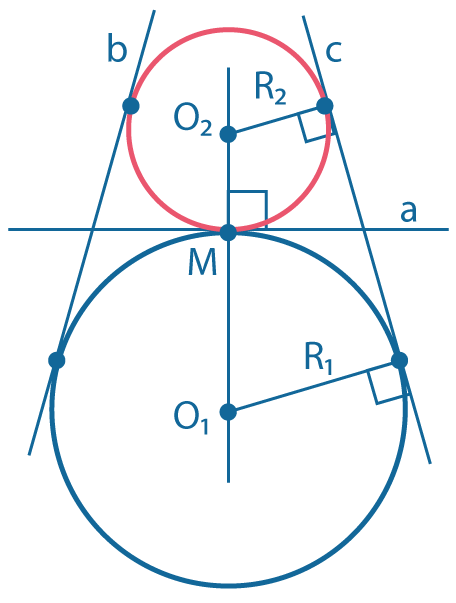Одна окружность касается другой снаружи - окружности имеют общую точку \(M\), лежащую на прямой \(O_1O_2\).
Есть три общих касательных.
Одна из них \((а)\) проходит через точку касания окружностей и перпендикулярапрямой \(O_1O_2\).
Если радиусы окружностей равны, то две другие общие касательные \((b~ и ~c) \) параллельны, а если радиусы не равны, то эти общие касательные пересекаются в точке, лежащей на прямой \(O_1O_2\).
Расстояние между центрами окружностей равно сумме их радиусов: \(O_1O_2=R_1+R_2\).

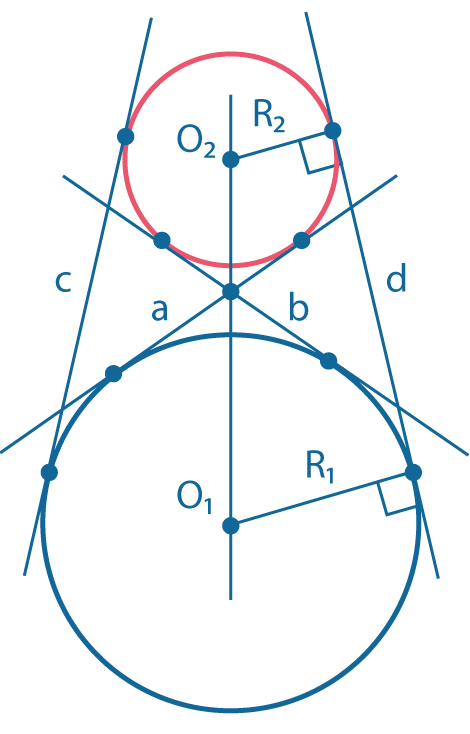Одна окружность лежит вне другой.
Есть четыре общих касательных: две из них \((a ~и ~b)\) называются внутренними и всегда пересекаются в точке, лежащей на отрезке \(O_1O_2\).
Две другие общие касательные \((c ~и ~d)\)называются внешними.
Если радиусы окружностей равны, то внешние касательные параллельны, а если радиусы не равны, то внешние касательные пересекаются в точке, лежащей на прямой \(O_1O_2\).
Расстояние между центрами окружностей больше суммы их радиусов: \(O_1O_2>R_1+R_2\)

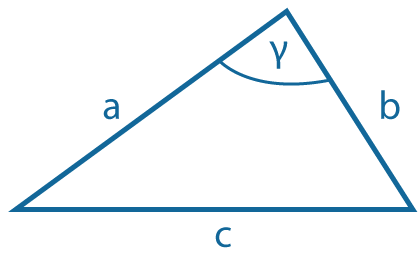Теорема косинусов:

\(c^2=a^2+b^2-2ab~cos γ\)

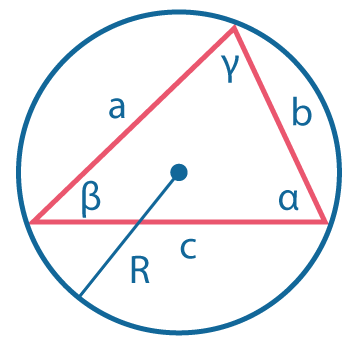Теорема синусов:

\({a \over sin~α}={b \over sin~β}={c \over sin~γ}\).

Это отношение равно \(2R\), где \(R\) - радиус описанной окружности.

Свойства биссектрис

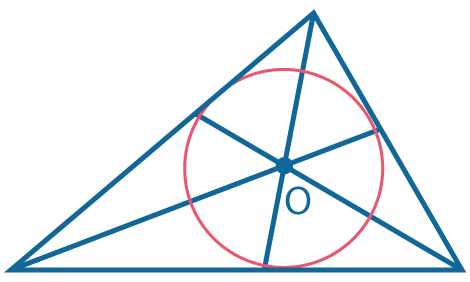Три биссектрисы пересекаются в одной точке, которая всегда лежит внутри треугольника.
Эта точка является центром вписанной окружности.

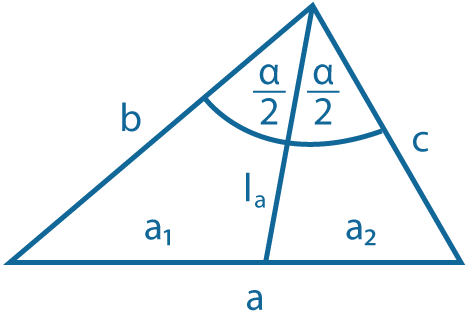Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам:

\( {a_1 \over a_2}= {b \over c}\)

Вписанная и описанная окружности

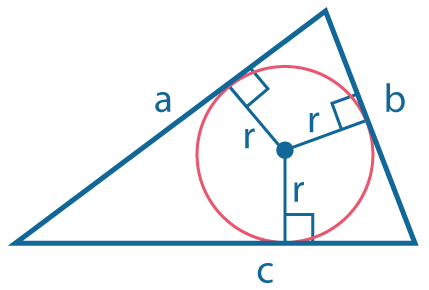В любой треугольник можно вписать окружность.
Центр вписанной окружности - точка пересечения биссектрис.
Радиус вписанной окружности:

\(r=S/p\), где \(S\) - площадь треугольника,
\(p={{a+b+c} \over2}\).

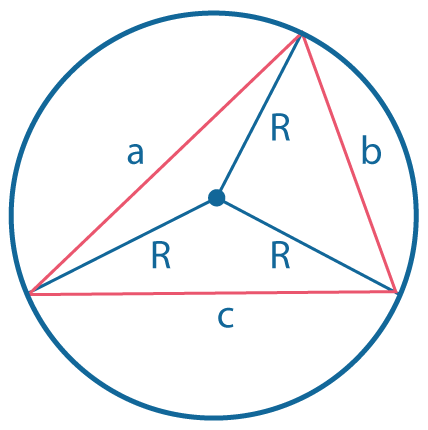Около любого треугольника можно описать окружность.
Центр описанной окружности - точка пересечения серединных перпендикуляров.
Радиус описанной окружности:

\(R= {abc \over 4S}\), где \(S\) - площадь треугольника.

Окружность, вписанная в прямоугольный треугольник

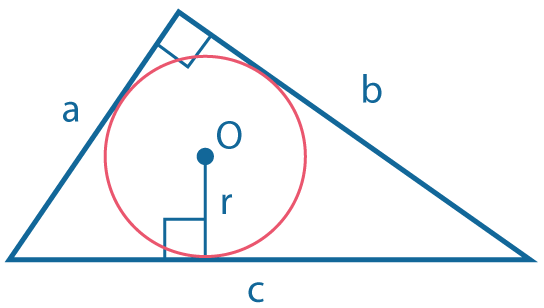Радиус вписанной окружности:

\(r={ab\over a+b+c}\),
\(r={a+b-c\over 2}\).

Центр описанной окружности совпадает с серединой гипотенузы, а радиус равен:

половине гипотенузы:
\(R = {c \over 2}\)
медиане, проведенной к гипотенузе:
\(R =m_c\)

Методические материалы к уроку

Для того, чтобы открыть методический материал, необходимо записаться на урок.

Практикум

Для прохождения домашнего задания, вам необходимо записаться на урок.

Филимонова Елена Викторовна

подробнее о преподавателе