«Академия»
О нас Об academiaRF.ru СМИ о нас Полезная информация Юридическая информация Курсы ОГЭ ЕГЭ Годовые курсы Экспресс-подготовка Русский язык Математика Обществознание Английский язык Лекции для родителей Преподаватели Косицына Евгения Федоровна Алексеева Вера Олеговна Бородкина Ольга Викторовна Новичкова Дана Александровна Филимонова Елена Викторовна Макарова Галина Юрьевна Раскина Дина Анатольевна Музычка Андрей Юрьевич Расписание Сегодня             Неделя             Месяц             Тесты Русский язык. ЕГЭ Русский язык. ОГЭ Математика. ЕГЭ Математика. ОГЭ Физика. ЕГЭ Обществознание. ЕГЭ Английский язык. B1 Досрочный ЕГЭ по математике 2017 Разбор Демо 2017 Русский язык Разбор Демо 2017 Математика Разбор Демо 2017 Обществознание Разбор Демо 2017 Английский язык Стоимость
Регистрация Вход
Бесплатно. ЕГЭ. Математика. Годовой курс 56 уроков, 112 часов
Задачи, основанные на теории чисел. Последняя задача ЕГЭ
03.10.16 16:00
Урок 1
Бесплатный
Вводное занятие. Натуральные числа
05.10.16 16:00
Урок 2
Бесплатный
Целые числа. Делимость с остатком. НОД и НОК
10.10.16 16:00
Урок 3
Бесплатный
Свойства НОД и НОК. Диофантовы уравнения
12.10.16 16:00
Урок 4
Бесплатный
Диофантовы уравнения второго порядка
Текстовые задачи
17.10.16 16:00
Урок 5
Бесплатный
Простейшие текстовые задачи
19.10.16 16:00
Урок 6
Бесплатный
Проценты
24.10.16 16:00
Урок 7
Бесплатный
Проценты. Формула сложных процентов
31.10.16 16:00
Урок 8
Бесплатный
Текстовые задачи на работу и движение
Теория вероятности
02.11.16 16:00
Урок 9
Бесплатный
Основные понятия теории вероятности
Корни, степени, логарифмы
07.11.16 16:00
Урок 10
Бесплатный
Степени и корни
09.11.16 16:00
Урок 11
Бесплатный
Понятие о логарифме
Решение уравнений
16.11.16 16:00
Урок 12
Бесплатный
Решение алгебраических уравнений
21.11.16 16:00
Урок 13
Бесплатный
Решение показательных и логарифмических уравнений
23.11.16 16:00
Урок 14
Бесплатный
Решение показательных и логарифмических уравнений
Тригонометрия
28.11.16 16:00
Урок 15
Бесплатный
Геометрическое определение тригонометрических функций. Тригонометрическая окружность
30.11.16 16:00
Урок 16
Бесплатный
Тригонометрические выражения
05.12.16 16:00
Урок 17
Бесплатный
Тригонометрические выражения. Продолжение
07.12.16 16:00
Урок 18
Бесплатный
Тригонометрические уравнения. Методы решения
12.12.16 16:00
Урок 19
Бесплатный
Методы решения тригонометрических уравнений. Продолжение
14.12.16 16:00
Урок 20
Бесплатный
Тригонометрические неравенства
Производная и начала математического анализа
19.12.16 16:00
Урок 21
Бесплатный
Определение производной
21.12.16 16:00
Урок 22
Бесплатный
Производная функции
11.01.17 16:00
Урок 23
Бесплатный
Возрастание и убывание функций. Задачи на экстремум
16.01.17 16:00
Урок 24
Бесплатный
Экономические задачи на наибольшее и наименьшее значения
18.01.17 16:00
Урок 25
Бесплатный
Экономические задачи (продолжение). Первообразная и интеграл
Планиметрия
23.01.17 16:00
Урок 26
Бесплатный
Координатная плоскость. Отрезки. Прямые. Углы и треугольники
25.01.17 16:00
Урок 27
Бесплатный
Треугольники
30.01.17 16:00
Урок 28
Бесплатный
Параллелограмм
01.02.17 16:00
Урок 29
Бесплатный
Трапеция. Четыреугольники. Векторы
06.02.17 16:00
Урок 30
Бесплатный
Окружность. Круг. Углы
08.02.17 16:00
Урок 31
Бесплатный
Окружности, связанные с треугольником, четырехугольником
13.02.17 16:00
Урок 32
Бесплатный
Задачи, связанные с окружностью
15.02.17 16:00
Урок 33
Бесплатный
Планиметрия. Повышенный уровень
20.02.17 16:00
Урок 34
Бесплатный
Планиметрия. Повышенный уровень
22.02.17 16:00
Урок 35
Бесплатный
Задачи с развернутым ответом
Стереометрия
27.02.17 16:00
Урок 36
Бесплатный
Куб. Параллелепипед
01.03.17 16:00
Урок 37
Бесплатный
Призма. Пирамида
06.03.17 16:00
Урок 38
Бесплатный
Тела вращения
13.03.17 16:00
Урок 39
Бесплатный
Комбинации тел
15.03.17 16:00
Урок 40
Бесплатный
Углы между плоскостями. Углы между прямыми
20.03.17 16:00
Урок 41
Бесплатный
Углы и расстояния в пространстве
22.03.17 16:00
Урок 42
Бесплатный
Комбинированные задачи на многогранники
27.03.17 16:00
Урок 43
Бесплатный
Стереометрия. Повышенный уровень
29.03.17 16:00
Урок 44
Бесплатный
Стереометрия. Повышенный уровень
Неравенства
03.04.17 16:00
Урок 45
Бесплатный
Обобщенный метод интервалов
05.04.17 16:00
Урок 46
Бесплатный
Неравенства, содержащие модули. Иррациональные неравенства
10.04.17 16:00
Урок 47
Бесплатный
Неравенства, содержащие модули. Иррациональные неравенства. Повышенная сложность
12.04.17 16:00
Урок 48
Бесплатный
Показательные неравенства
17.04.17 16:00
Урок 49
Бесплатный
Логарифмические неравенства
19.04.17 16:00
Урок 50
Бесплатный
Разбор досрочного варианта ЕГЭ 2017
24.04.17 16:00
Урок 51
Бесплатный
Комбинированные неравенства
Задачи с параметром
26.04.17 16:00
Урок 52
Бесплатный
Задачи с параметром
15.05.17 16:00
Урок 53
Бесплатный
Задачи с параметром
17.05.17 16:00
Урок 54
Бесплатный
Задачи с параметром
22.05.17 16:00
Урок 55
Бесплатный
Задачи с параметром
24.05.17 18:00
Урок 56
Бесплатный
Разбор ЕГЭ
Урок 35. Задачи с развернутым ответом

Сечение многогранника плоскостью

Урок завершен 22 февраля в 16:00
Записаться на открытый урок
Задачи с развернутым ответом

Урок

Смотреть запись урока  

Теория

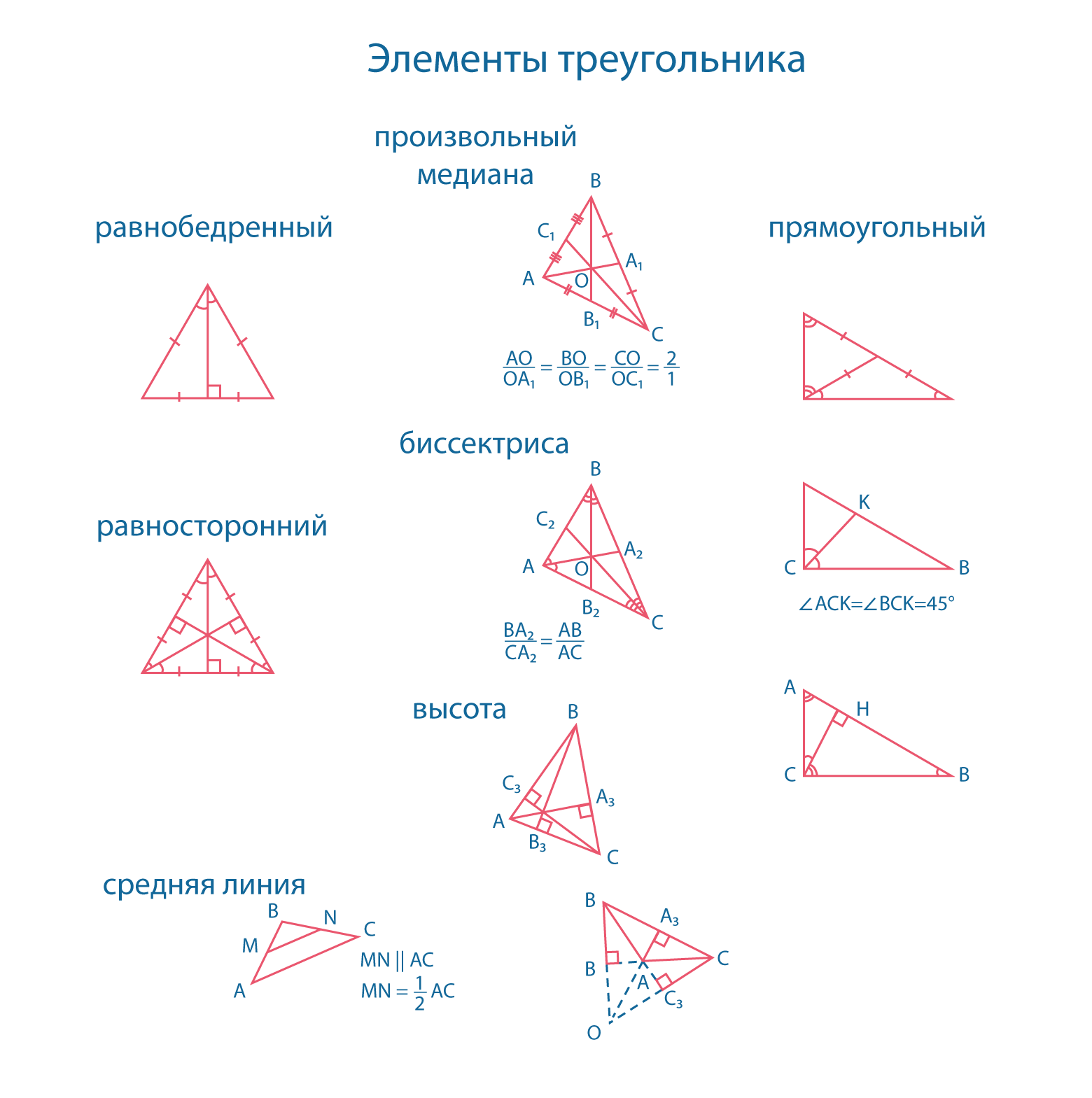
Подобие треугольников

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.

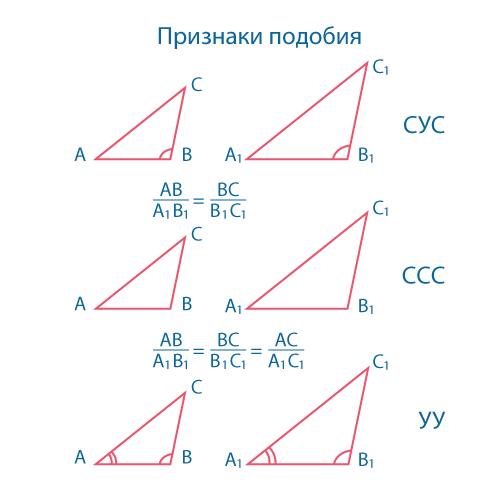
Высота в прямоугольном треугольнике образует три подобных треугольника:

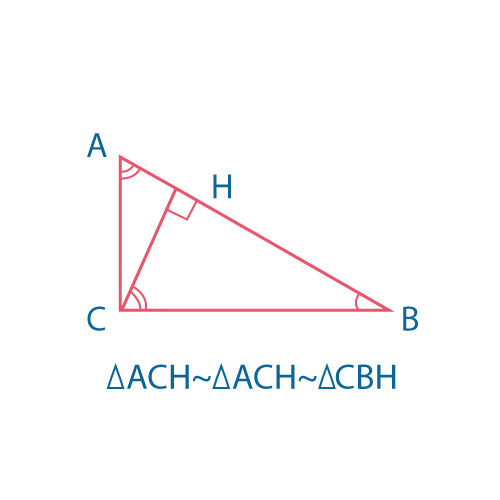
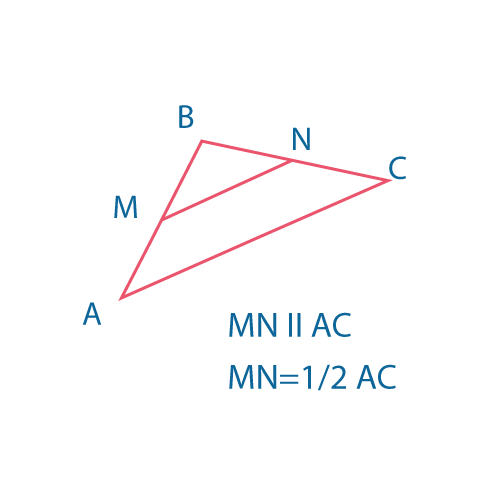
Средняя линия треугольника соединяет середины двух его сторон. Средняя линия треугольника параллельна основанию и равна его половине.

Площадь треугольника

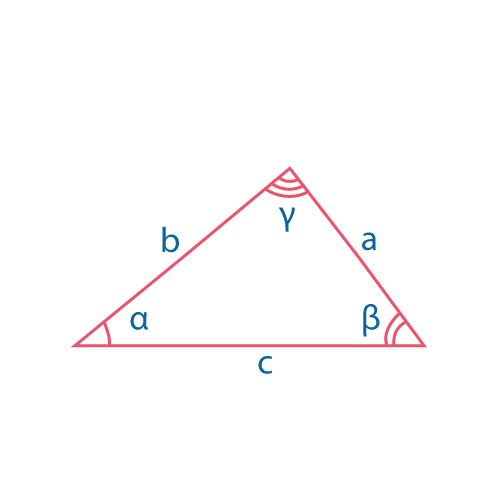
\(S={1\over 2}a\cdot h_a={1\over 2}b\cdot h_b={1\over 2}c\cdot h_c\)

\(S={1\over 2}absinγ={1\over 2}bcsinα={1\over 2}acsinβ\)

\(S= \sqrt{p(p-a)(p-b)(p-c)}\), где \(p={{a+b+c}\over 2}\)

 

Теорема синусов и теорема косинусов

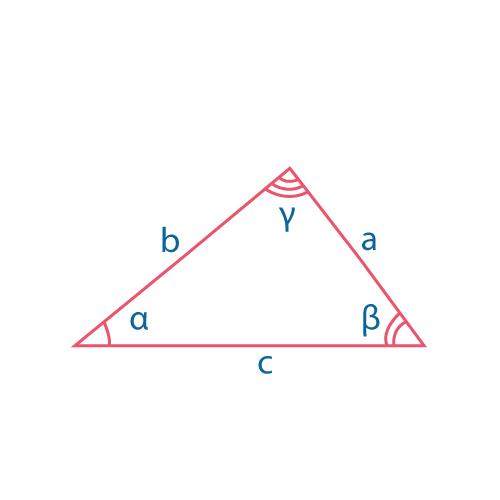
\({a\over sinα}={b\over sinβ}={c\over sinγ}\)

\(a^2=b^2+c^2-2bc\cdot cosα\)

 

Площадь параллелограмма

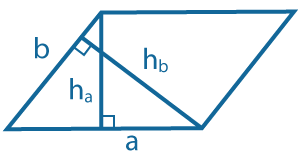Через сторону и опущенную на нее высоту:

\(S=ah_a=bh_b\)

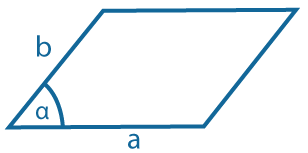Через две прилежащие стороны и угол между ними:

\(S=ab~sin~α\)

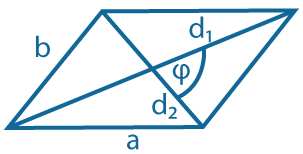Через диагонали и угол между ними:

\(S = {d_1d_2~sin\varphi \over 2}\)

Методические материалы к уроку

Для того, чтобы открыть методический материал, необходимо записаться на урок.

Практикум

Для прохождения домашнего задания, вам необходимо записаться на урок.
Филимонова Елена Викторовна
подробнее о преподавателе
3 октября в 16:00
Урок 1
Вводное занятие. Натуральные числа
5 октября в 16:00
Урок 2
Целые числа. Делимость с остатком. НОД и НОК
10 октября в 16:00
Урок 3
Свойства НОД и НОК. Диофантовы уравнения
12 октября в 16:00
Урок 4
Диофантовы уравнения второго порядка
17 октября в 16:00
Урок 5
Простейшие текстовые задачи
19 октября в 16:00
Урок 6
Проценты
24 октября в 16:00
Урок 7
Проценты. Формула сложных процентов
31 октября в 16:00
Урок 8
Текстовые задачи на работу и движение
2 ноября в 16:00
Урок 9
Основные понятия теории вероятности
7 ноября в 16:00
Урок 10
Степени и корни
9 ноября в 16:00
Урок 11
Понятие о логарифме
16 ноября в 16:00
Урок 12
Решение алгебраических уравнений
21 ноября в 16:00
Урок 13
Решение показательных и логарифмических уравнений
23 ноября в 16:00
Урок 14
Решение показательных и логарифмических уравнений
28 ноября в 16:00
Урок 15
Геометрическое определение тригонометрических функций. Тригонометрическая окружность
30 ноября в 16:00
Урок 16
Тригонометрические выражения
5 декабря в 16:00
Урок 17
Тригонометрические выражения. Продолжение
7 декабря в 16:00
Урок 18
Тригонометрические уравнения. Методы решения
12 декабря в 16:00
Урок 19
Методы решения тригонометрических уравнений. Продолжение
14 декабря в 16:00
Урок 20
Тригонометрические неравенства
19 декабря в 16:00
Урок 21
Определение производной
21 декабря в 16:00
Урок 22
Производная функции
11 января в 16:00
Урок 23
Возрастание и убывание функций. Задачи на экстремум
16 января в 16:00
Урок 24
Экономические задачи на наибольшее и наименьшее значения
18 января в 16:00
Урок 25
Экономические задачи (продолжение). Первообразная и интеграл
23 января в 16:00
Урок 26
Координатная плоскость. Отрезки. Прямые. Углы и треугольники
25 января в 16:00
Урок 27
Треугольники
30 января в 16:00
Урок 28
Параллелограмм
1 февраля в 16:00
Урок 29
Трапеция. Четыреугольники. Векторы
6 февраля в 16:00
Урок 30
Окружность. Круг. Углы
8 февраля в 16:00
Урок 31
Окружности, связанные с треугольником, четырехугольником
13 февраля в 16:00
Урок 32
Задачи, связанные с окружностью
15 февраля в 16:00
Урок 33
Планиметрия. Повышенный уровень
20 февраля в 16:00
Урок 34
Планиметрия. Повышенный уровень
22 февраля в 16:00
Урок 35
Задачи с развернутым ответом
27 февраля в 16:00
Урок 36
Куб. Параллелепипед
1 марта в 16:00
Урок 37
Призма. Пирамида
6 марта в 16:00
Урок 38
Тела вращения
13 марта в 16:00
Урок 39
Комбинации тел
15 марта в 16:00
Урок 40
Углы между плоскостями. Углы между прямыми
20 марта в 16:00
Урок 41
Углы и расстояния в пространстве
22 марта в 16:00
Урок 42
Комбинированные задачи на многогранники
27 марта в 16:00
Урок 43
Стереометрия. Повышенный уровень
29 марта в 16:00
Урок 44
Стереометрия. Повышенный уровень
3 апреля в 16:00
Урок 45
Обобщенный метод интервалов
5 апреля в 16:00
Урок 46
Неравенства, содержащие модули. Иррациональные неравенства
10 апреля в 16:00
Урок 47
Неравенства, содержащие модули. Иррациональные неравенства. Повышенная сложность
12 апреля в 16:00
Урок 48
Показательные неравенства
17 апреля в 16:00
Урок 49
Логарифмические неравенства
19 апреля в 16:00
Урок 50
Разбор досрочного варианта ЕГЭ 2017
24 апреля в 16:00
Урок 51
Комбинированные неравенства
26 апреля в 16:00
Урок 52
Задачи с параметром
15 мая в 16:00
Урок 53
Задачи с параметром
17 мая в 16:00
Урок 54
Задачи с параметром
22 мая в 16:00
Урок 55
Задачи с параметром
24 мая в 18:00
Урок 56
Разбор ЕГЭ
119334, г. Москва,
Ленинский пр-т, 32а
Пн. – Пт.
10.00 – 20.00
  Технические требования
  Юридическая информация
  Партнерская программа
  Договор оферты
vk
ok instagram
Пишите нам:
Федеральная программа онлайн-обучения для школьников: возможность получить образование столичного уровня в регионах России.
Формула проекта разработана в лаборатории Mitlabs © 2019. Все права защищены.