Расстояние от точки до плоскости

Простейшие текстовые задачи

Проценты. Формула сложных процентов

31.10.16 16:00

Урок 8

Текстовые задачи на работу и движение

Теория вероятности

02.11.16 16:00

Урок 9

Основные понятия теории вероятности

Корни, степени, логарифмы

Решение уравнений

Решение алгебраических уравнений

21.11.16 16:00

Урок 13

23.11.16 16:00

Урок 14

Тригонометрия

28.11.16 16:00

Урок 15

Геометрическое определение тригонометрических функций. Тригонометрическая окружность

30.11.16 16:00

Урок 16

Тригонометрические выражения

05.12.16 16:00

Урок 17

Тригонометрические выражения. Продолжение

07.12.16 16:00

Урок 18

Тригонометрические уравнения. Методы решения

12.12.16 16:00

Урок 19

Методы решения тригонометрических уравнений. Продолжение

14.12.16 16:00

Урок 20

Тригонометрические неравенства

Производная и начала математического анализа

19.12.16 16:00

Урок 21

Возрастание и убывание функций. Задачи на экстремум

Определение производной

16.01.17 16:00

Урок 24

Экономические задачи на наибольшее и наименьшее значения

18.01.17 16:00

Урок 25

Экономические задачи (продолжение). Первообразная и интеграл

Планиметрия

23.01.17 16:00

Урок 26

Координатная плоскость. Отрезки. Прямые. Углы и треугольники

Трапеция. Четыреугольники. Векторы

06.02.17 16:00

Урок 30

Окружность. Круг. Углы

08.02.17 16:00

Урок 31

Окружности, связанные с треугольником, четырехугольником

13.02.17 16:00

Урок 32

Задачи, связанные с окружностью

15.02.17 16:00

Урок 33

20.02.17 16:00

Урок 34

22.02.17 16:00

Урок 35

Задачи с развернутым ответом

Стереометрия

27.02.17 16:00

Урок 36

Бесплатный

Куб. Параллелепипед

Углы между плоскостями. Углы между прямыми

20.03.17 16:00

Урок 41

Углы и расстояния в пространстве

22.03.17 16:00

Урок 42

Комбинированные задачи на многогранники

27.03.17 16:00

Урок 43

29.03.17 16:00

Урок 44

Неравенства

03.04.17 16:00

Урок 45

Обобщенный метод интервалов

05.04.17 16:00

Урок 46

Неравенства, содержащие модули. Иррациональные неравенства

10.04.17 16:00

Урок 47

Неравенства, содержащие модули. Иррациональные неравенства. Повышенная сложность

12.04.17 16:00

Урок 48

Показательные неравенства

17.04.17 16:00

Урок 49

Логарифмические неравенства

19.04.17 16:00

Урок 50

Разбор досрочного варианта ЕГЭ 2017

24.04.17 16:00

Урок 51

Комбинированные неравенства

Задачи с параметром

Урок 36. Куб. Параллелепипед

Расстояние от точки до плоскости

Урок завершен 27 февраля в 16:00

Записаться на открытый урок

Куб. Параллелепипед. Площади. Объемы

Урок

Смотреть запись урока

Теория

Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.

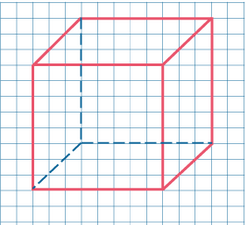
Свойства куба:

1. В кубе 6 граней и все они являются квадратами.

2. Противоположные грани попарно параллельны.

3. Все двугранные углы куба – прямые.

4. Диагонали равны.

5. Куб имеет 4 диагонали, которые пересекаются в одной точке и делятся в ней пополам.

6. Диагональ куба в \(\sqrt{3}\) раз больше его ребра

7. Диагональ грани куба в \(\sqrt{2}\) раза больше длины ребра.

Пусть а−длина ребра куба, d−диагональ куба, тогда справедливы формулы:

Объем куба: \(V=a^3= {d^3 \over 3\sqrt{3}}\)

Площадь полной поверхности: \(S=6a^2= {2d^2}\)

Прямоугольный параллелепипед

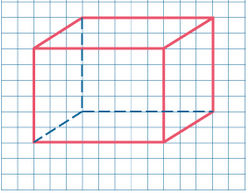
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

а- длина;

b- ширина;

с- высота (она же боковое ребро);

Объем равен: \(V=abc\)

Площадь полной поверхности: \(S=2(ab+bc+ac)\)

Произвольный параллелепипед

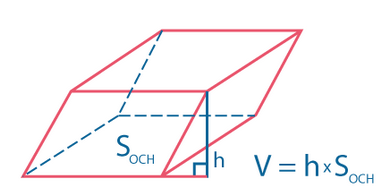
Площади поверхностей

Площадь поверхности – это сумма площадей всех граней.

Площадь боковой поверхности – это сумма площадей всех боковых граней.

При изменении всех линейных размеров в \(k\) раз площадь поверхности тела увеличивается в \(k^2\) раз.

Объемы

При изменении всех линейных размеров в \(k\) раз объём тела увеличивается в \(k^3\) раз.

Методические материалы к уроку

Для того, чтобы открыть методический материал, необходимо записаться на урок.

Практикум

Для прохождения домашнего задания, вам необходимо записаться на урок.

Филимонова Елена Викторовна

подробнее о преподавателе

3 октября в 16:00

Урок 1

Вводное занятие. Натуральные числа

5 октября в 16:00

Урок 2

Целые числа. Делимость с остатком. НОД и НОК

10 октября в 16:00

Урок 3

Свойства НОД и НОК. Диофантовы уравнения

12 октября в 16:00

Урок 4

Диофантовы уравнения второго порядка

17 октября в 16:00

Урок 5

Простейшие текстовые задачи

Проценты. Формула сложных процентов

31 октября в 16:00

Урок 8

Текстовые задачи на работу и движение

2 ноября в 16:00

Урок 9

Основные понятия теории вероятности

Решение алгебраических уравнений

21 ноября в 16:00

Урок 13

23 ноября в 16:00

Урок 14

Геометрическое определение тригонометрических функций. Тригонометрическая окружность

28 ноября в 16:00

Урок 15

30 ноября в 16:00

Урок 16

Тригонометрические выражения

5 декабря в 16:00

Урок 17

Тригонометрические выражения. Продолжение

7 декабря в 16:00

Урок 18

Тригонометрические уравнения. Методы решения

12 декабря в 16:00

Урок 19

Методы решения тригонометрических уравнений. Продолжение

14 декабря в 16:00

Урок 20

Тригонометрические неравенства

19 декабря в 16:00

Урок 21

Определение производной

Возрастание и убывание функций. Задачи на экстремум

16 января в 16:00

Урок 24

Экономические задачи на наибольшее и наименьшее значения

18 января в 16:00

Урок 25

Экономические задачи (продолжение). Первообразная и интеграл

23 января в 16:00

Урок 26

Координатная плоскость. Отрезки. Прямые. Углы и треугольники

Трапеция. Четыреугольники. Векторы

6 февраля в 16:00

Урок 30

Окружность. Круг. Углы

8 февраля в 16:00

Урок 31

Окружности, связанные с треугольником, четырехугольником

13 февраля в 16:00

Урок 32

Задачи, связанные с окружностью

15 февраля в 16:00

Урок 33

20 февраля в 16:00

Урок 34

Задачи с развернутым ответом

22 февраля в 16:00

Урок 35

Углы между плоскостями. Углы между прямыми

20 марта в 16:00

Урок 41

Углы и расстояния в пространстве

22 марта в 16:00

Урок 42

Комбинированные задачи на многогранники

27 марта в 16:00

Урок 43

29 марта в 16:00

Урок 44