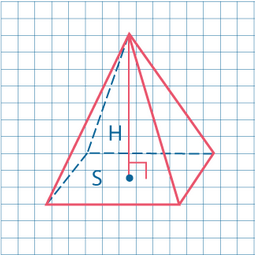
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) - треугольники, имеющие общую вершину.

Высотой (h) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Формулы вычмсления объема и площади поверхности правильной пирамиды:

\(S_{бок} = {P_{осн} h_{a} \over 2}\)

\(S_{п.п.} = S_{бок}+S_{осн}\)

\(V= {1 \over 3}{S_{осн} h }\)

Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.

Свойства правильной треугольной пирамиды:

- боковые ребра правильной пирамиды равны

- все боковые грани правильной пирамиды являются равнобедренными треугольниками

- в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу

- если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (60 градусов ).

- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

Тетраэдр - это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.

У тетраэдра:

- Все грани равны

- 4 грани, 4 вершины и 6 ребер

- Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

Призма

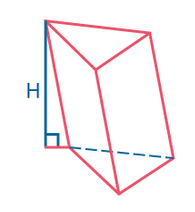
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и n-го количества параллелограммов.

Многоугольники – называются основаниями призмы.

Параллелограммы - боковыми гранями.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

\(S_{бок} = {P_{осн} h}\)

\(S_{п.п.} = S_{бок}+2S_{осн}\)

\(V= {S_{осн} h }\)