
Ленинский пр-т, 32а
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
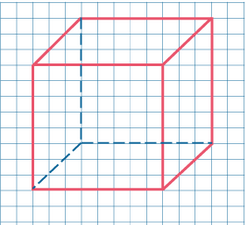
Свойства куба:
1. В кубе 6 граней и все они являются квадратами.
2. Противоположные грани попарно параллельны.
3. Все двугранные углы куба – прямые.
4. Диагонали равны.
5. Куб имеет 4 диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Диагональ куба в \(\sqrt{3}\) раз больше его ребра
7. Диагональ грани куба в \(\sqrt{2}\) раза больше длины ребра.
Пусть а−длина ребра куба, d−диагональ куба, тогда справедливы формулы:
Объем куба: \(V=a^3= {d^3 \over 3\sqrt{3}}\)
Площадь полной поверхности: \(S=6a^2= {2d^2}\)
Прямоугольный параллелепипед
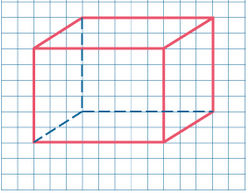
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
а- длина;
b- ширина;
с- высота (она же боковое ребро);
Объем равен: \(V=abc\)
Площадь полной поверхности: \(S=2(ab+bc+ac)\)
Произвольный параллелепипед
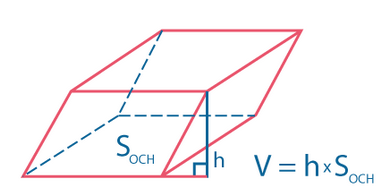
Площади поверхностей
Площадь поверхности – это сумма площадей всех граней.
Площадь боковой поверхности – это сумма площадей всех боковых граней.
При изменении всех линейных размеров в \(k\) раз площадь поверхности тела увеличивается в \(k^2\) раз.
Объемы
При изменении всех линейных размеров в \(k\) раз объём тела увеличивается в \(k^3\) раз.
Пирамида
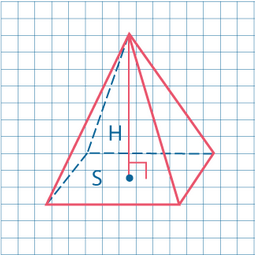
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) - треугольники, имеющие общую вершину.
Высотой (h) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Формулы вычмсления объема и площади поверхности правильной пирамиды:
\(S_{бок} = {P_{осн} h_{a} \over 2}\)
\(S_{п.п.} = S_{бок}+S_{осн}\)
\(V= {1 \over 3}{S_{осн} h }\)
Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
Свойства правильной треугольной пирамиды:
- боковые ребра правильной пирамиды равны
- все боковые грани правильной пирамиды являются равнобедренными треугольниками
- в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
- если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (60 градусов ).
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
Тетраэдр - это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.
У тетраэдра:
- Все грани равны
- 4 грани, 4 вершины и 6 ребер
- Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
Призма
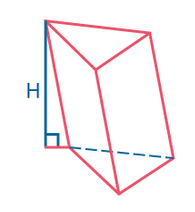
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и n-го количества параллелограммов.
Многоугольники – называются основаниями призмы.
Параллелограммы - боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
\(S_{бок} = {P_{осн} h}\)
\(S_{п.п.} = S_{бок}+2S_{осн}\)
\(V= {S_{осн} h }\)
Цилиндр
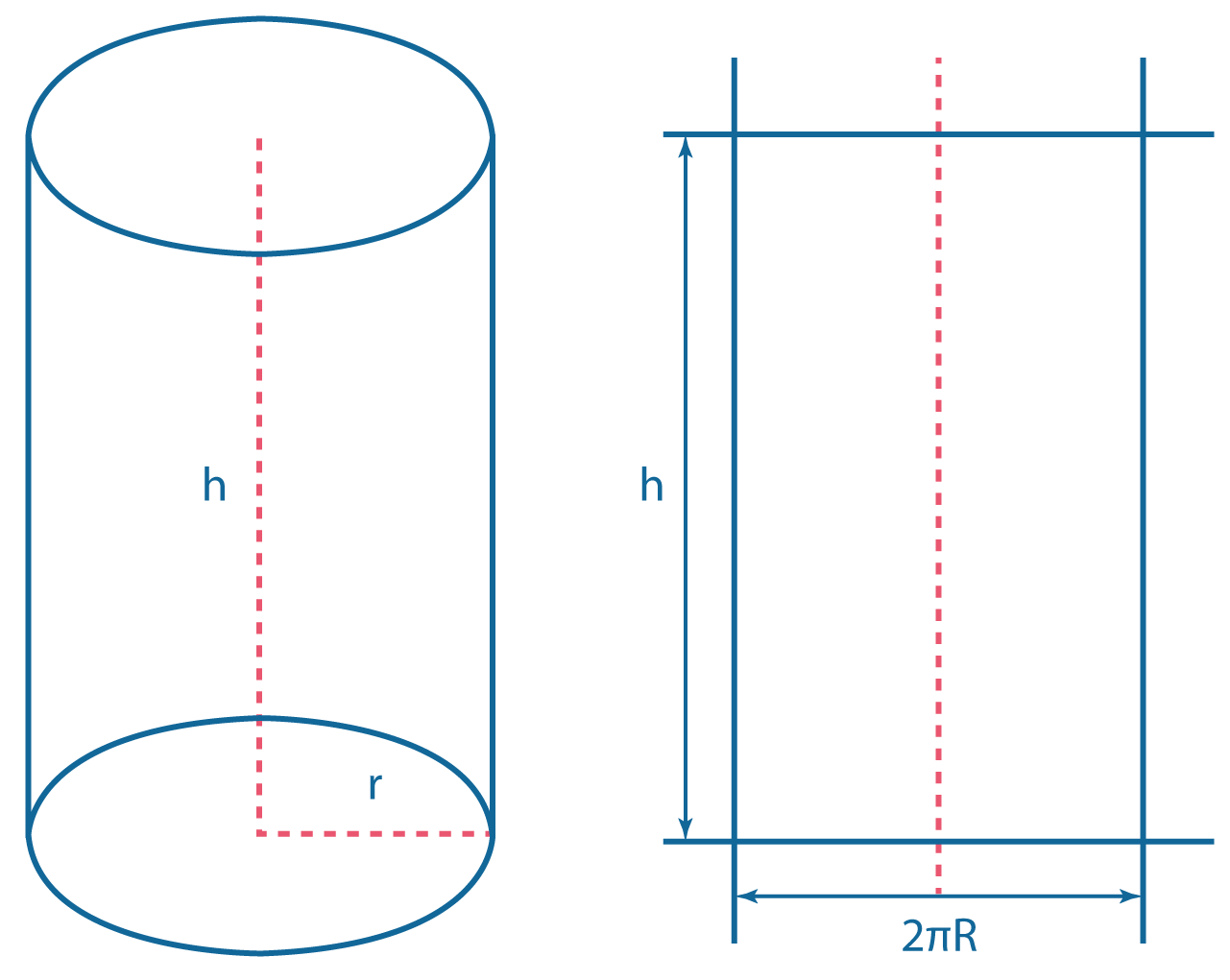
Тело, образующееся при вращении прямоугольника вокруг прямой, включающей в себя его сторону.
\(L\) — образующая.
\(V= hπr^2\)
\(S_{бп}=2πrh\)
Конус
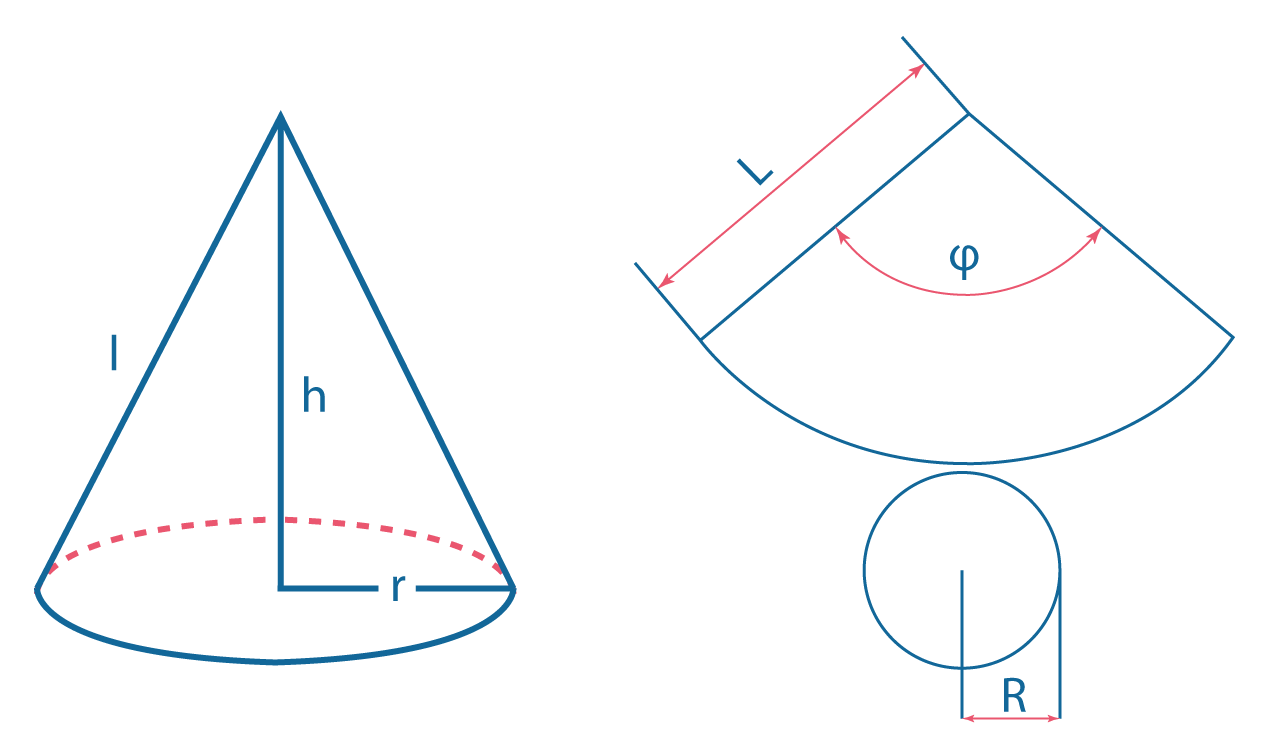
Тело, образующееся при вращении прямоугольного треугольника вокруг прямой, включающей в себя его катет.
\(L\) — образующая.
\(V= {1 \over 3}πr^2\)
\(S_{бп}=πrl\)
Шар
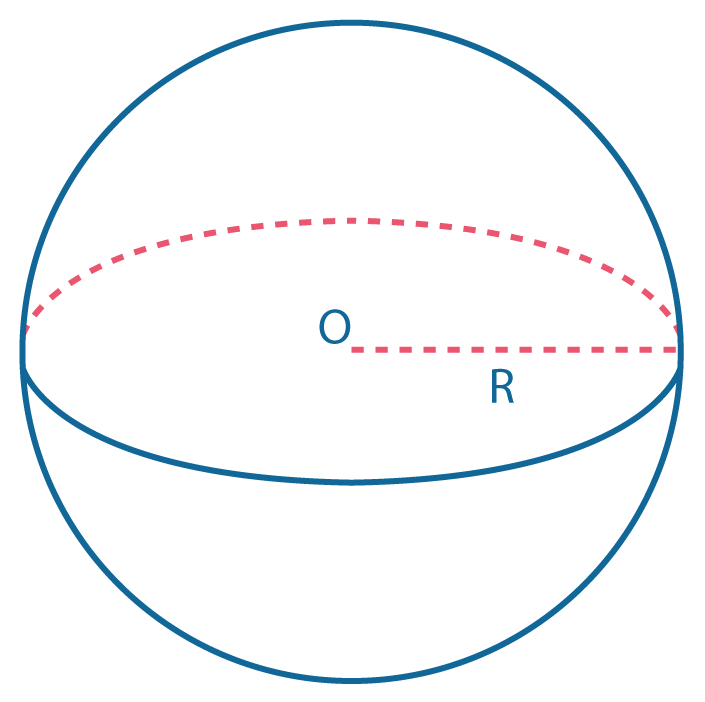
Шар — это совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного центра.
\(V= {4 \over 3}πr^3\)
\(S_{сферы}=4πr^2\)