«Академия»

О нас Об academiaRF.ru СМИ о нас Полезная информация Юридическая информация Курсы ОГЭ ЕГЭ Годовые курсы Экспресс-подготовка Русский язык Математика Обществознание Английский язык Лекции для родителей Преподаватели Косицына Евгения Федоровна Алексеева Вера Олеговна Бородкина Ольга Викторовна Новичкова Дана Александровна Филимонова Елена Викторовна Макарова Галина Юрьевна Раскина Дина Анатольевна Музычка Андрей Юрьевич Расписание Сегодня Неделя Месяц Тесты Русский язык. ЕГЭ Русский язык. ОГЭ Математика. ЕГЭ Математика. ОГЭ Физика. ЕГЭ Обществознание. ЕГЭ Английский язык. B1 Досрочный ЕГЭ по математике 2017 Разбор Демо 2017 Русский язык Разбор Демо 2017 Математика Разбор Демо 2017 Обществознание Разбор Демо 2017 Английский язык Стоимость

Регистрация Вход

Бесплатно. ЕГЭ. Математика. Годовой курс 56 уроков, 112 часов

Задачи, основанные на теории чисел. Последняя задача ЕГЭ

Бесплатный

Вводное занятие. Натуральные числа

Бесплатный

Целые числа. Делимость с остатком. НОД и НОК

Бесплатный

Свойства НОД и НОК. Диофантовы уравнения

Бесплатный

Диофантовы уравнения второго порядка

Текстовые задачи

Бесплатный

Простейшие текстовые задачи

Бесплатный

Проценты

Бесплатный

Проценты. Формула сложных процентов

Бесплатный

Текстовые задачи на работу и движение

Теория вероятности

Бесплатный

Основные понятия теории вероятности

Корни, степени, логарифмы

Бесплатный

Степени и корни

Бесплатный

Понятие о логарифме

Решение уравнений

Бесплатный

Решение алгебраических уравнений

Бесплатный

Решение показательных и логарифмических уравнений

Бесплатный

Решение показательных и логарифмических уравнений

Тригонометрия

Бесплатный

Геометрическое определение тригонометрических функций. Тригонометрическая окружность

Бесплатный

Тригонометрические выражения

Бесплатный

Тригонометрические выражения. Продолжение

Бесплатный

Тригонометрические уравнения. Методы решения

Бесплатный

Методы решения тригонометрических уравнений. Продолжение

Бесплатный

Тригонометрические неравенства

Производная и начала математического анализа

Бесплатный

Определение производной

Бесплатный

Производная функции

Бесплатный

Возрастание и убывание функций. Задачи на экстремум

Бесплатный

Экономические задачи на наибольшее и наименьшее значения

Бесплатный

Экономические задачи (продолжение). Первообразная и интеграл

Планиметрия

Бесплатный

Координатная плоскость. Отрезки. Прямые. Углы и треугольники

Бесплатный

Треугольники

Бесплатный

Параллелограмм

Бесплатный

Трапеция. Четыреугольники. Векторы

Бесплатный

Окружность. Круг. Углы

Бесплатный

Окружности, связанные с треугольником, четырехугольником

Бесплатный

Задачи, связанные с окружностью

Бесплатный

Планиметрия. Повышенный уровень

Бесплатный

Планиметрия. Повышенный уровень

Бесплатный

Задачи с развернутым ответом

Стереометрия

Бесплатный

Куб. Параллелепипед

Бесплатный

Призма. Пирамида

Бесплатный

Тела вращения

Бесплатный

Комбинации тел

Бесплатный

Углы между плоскостями. Углы между прямыми

20.03.17 16:00

Урок 41

Бесплатный

Углы и расстояния в пространстве

Бесплатный

Комбинированные задачи на многогранники

Бесплатный

Стереометрия. Повышенный уровень

Бесплатный

Стереометрия. Повышенный уровень

Неравенства

Бесплатный

Обобщенный метод интервалов

Бесплатный

Неравенства, содержащие модули. Иррациональные неравенства

Бесплатный

Неравенства, содержащие модули. Иррациональные неравенства. Повышенная сложность

Бесплатный

Показательные неравенства

Бесплатный

Логарифмические неравенства

Бесплатный

Разбор досрочного варианта ЕГЭ 2017

Бесплатный

Комбинированные неравенства

Задачи с параметром

Бесплатный

Задачи с параметром

Бесплатный

Задачи с параметром

Бесплатный

Задачи с параметром

Бесплатный

Задачи с параметром

Бесплатный

Разбор ЕГЭ

Урок 41. Углы и расстояния в пространстве

Расстояние в пространстве и метод объемов

Урок завершен 20 марта в 16:00

Записаться на открытый урок

Углы и расстояния в пространстве.

Урок

Смотреть запись урока

Теория

Расстояние между точками

Расстояние между точками – длина отрезка.

Можно пользоваться всеми фактами планиметрии. Чаще всего необходимы теорема Пифагора, соотношения между сторонами и углами в прямоугольном треугольнике, подобие треугольников и теорема косинусов.

Расстояние от точки до прямой

Расстояние от точки до прямой – это перпендикуляр, опущенный из точки на данную прямую.

Расстояние между параллельными прямыми – перпендикуляр, опущенный из любой точки одной прямой на другую прямую.

При поиске расстояния от точки до прямой можно перенести неудобную точку в удобное место!

Последовательность действий: построить прямую, параллельную данной и проходящую через заданную точку. Выбрать на этой прямой точку, из которой удобно опустить перпендикуляр на исходную прямую.

Расстояние от точки до плоскости – длина перпендикуляра, опущенного на плоскость.

Точки тоже можно переносить по параллельным прямым.

Также можно переносить по параллельным плоскостям.

Метод объемов

\(V_{пирамиды}={1\over 3} h\cdot S_{осн}\)

Высота – это перпендикуляр, опущенный из вершины на площадь основания пирамиды. То есть длина высоты – это расстояние от вершины пирамиды до плоскости основания.

У треугольной пирамиды основанием может быть любая грань. Следовательно, можно найти объём, вычислив удобную высоту и удобную площадь грани, а затем выразить необходимую высоту.

Расстояние между скрещивающимися прямыми

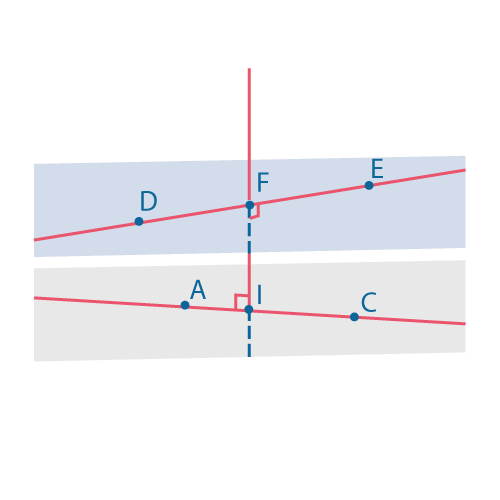
Расстояние между скрещивающимися прямыми – длина общего перпендикуляра.

Удобно искать общий перпендикуляр, если легко найти плоскость, перпендикулярную одной из прямых и проходящую через другую прямую.

Длина общего перпендикуляра равна также:

Расстоянию между прямой и параллельной ей плоскостью, проходящей через вторую прямую.

Расстоянию между двумя параллельными плоскостями, содержащими скрещивающиеся прямые.

Угол между скрещивающимися прямыми

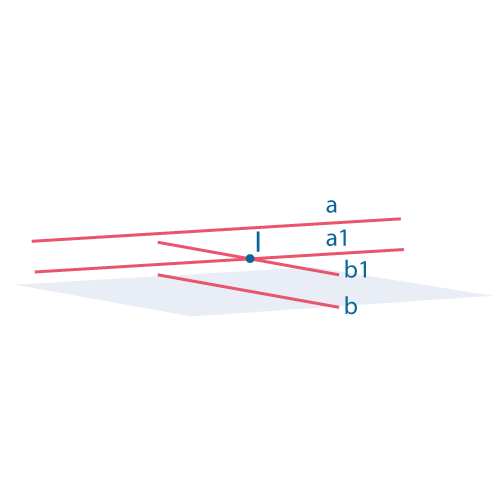
Угол между скрещивающимися прямыми \(a\) и \(b\) — это угол между пересекающимися прямыми \(a_1\) и \(b_1\), такими, что \(a_1|| a\) и \(b_1|| b\).

Также, одна из прямых \(a_1\) или \(b_1\) может совпадать с прямыми \(a\) или \(b\) соответственно.

Угол между прямой и плоскостью

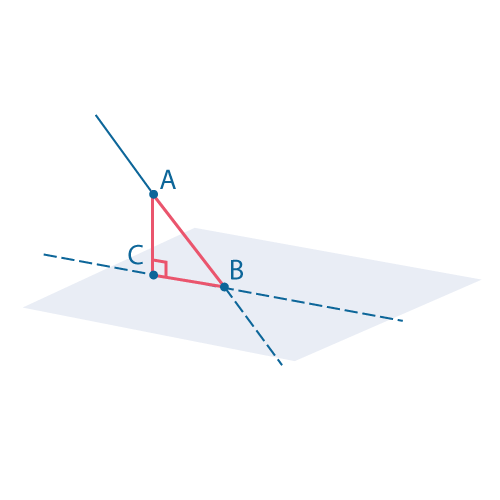
Если прямая \(a\) перпендикулярна плоскости \(α\), то угол между \(a\) и \(α\) равен \(90⁰\).

Если прямая \(a\) наклонена к плоскости \(α\), то угол между \(a\) и \(α\) равен углу между прямой \(a\) и её проекцией на плоскость \(α\).

Методические материалы к уроку

Для того, чтобы открыть методический материал, необходимо записаться на урок.

Практикум

Для прохождения домашнего задания, вам необходимо записаться на урок.

Филимонова Елена Викторовна

подробнее о преподавателе

3 октября в 16:00

Вводное занятие. Натуральные числа

5 октября в 16:00

Целые числа. Делимость с остатком. НОД и НОК

10 октября в 16:00

Свойства НОД и НОК. Диофантовы уравнения

12 октября в 16:00

Диофантовы уравнения второго порядка

17 октября в 16:00

Простейшие текстовые задачи

19 октября в 16:00

Проценты

24 октября в 16:00

Проценты. Формула сложных процентов

31 октября в 16:00

Текстовые задачи на работу и движение

2 ноября в 16:00

Основные понятия теории вероятности

7 ноября в 16:00

Степени и корни

9 ноября в 16:00

Понятие о логарифме

16 ноября в 16:00

Решение алгебраических уравнений

21 ноября в 16:00

Решение показательных и логарифмических уравнений

23 ноября в 16:00

Решение показательных и логарифмических уравнений

28 ноября в 16:00

Геометрическое определение тригонометрических функций. Тригонометрическая окружность

30 ноября в 16:00

Тригонометрические выражения

5 декабря в 16:00

Тригонометрические выражения. Продолжение

7 декабря в 16:00

Тригонометрические уравнения. Методы решения

12 декабря в 16:00

Методы решения тригонометрических уравнений. Продолжение

14 декабря в 16:00

Тригонометрические неравенства

19 декабря в 16:00

Определение производной

21 декабря в 16:00

Производная функции

11 января в 16:00

Возрастание и убывание функций. Задачи на экстремум

16 января в 16:00

Экономические задачи на наибольшее и наименьшее значения

18 января в 16:00

Экономические задачи (продолжение). Первообразная и интеграл

23 января в 16:00

Координатная плоскость. Отрезки. Прямые. Углы и треугольники

25 января в 16:00

Треугольники

30 января в 16:00

Параллелограмм

1 февраля в 16:00

Трапеция. Четыреугольники. Векторы

6 февраля в 16:00

Окружность. Круг. Углы

8 февраля в 16:00

Окружности, связанные с треугольником, четырехугольником

13 февраля в 16:00

Задачи, связанные с окружностью

15 февраля в 16:00

Планиметрия. Повышенный уровень

20 февраля в 16:00

Планиметрия. Повышенный уровень

22 февраля в 16:00

Задачи с развернутым ответом

27 февраля в 16:00

Куб. Параллелепипед

1 марта в 16:00

Призма. Пирамида

6 марта в 16:00

Тела вращения

13 марта в 16:00

Комбинации тел

15 марта в 16:00

Углы между плоскостями. Углы между прямыми

20 марта в 16:00

Углы и расстояния в пространстве

22 марта в 16:00

Комбинированные задачи на многогранники

27 марта в 16:00

Стереометрия. Повышенный уровень

29 марта в 16:00

Стереометрия. Повышенный уровень

3 апреля в 16:00

Обобщенный метод интервалов

5 апреля в 16:00

Неравенства, содержащие модули. Иррациональные неравенства

10 апреля в 16:00

Неравенства, содержащие модули. Иррациональные неравенства. Повышенная сложность

12 апреля в 16:00

Показательные неравенства

17 апреля в 16:00

Логарифмические неравенства

19 апреля в 16:00

Разбор досрочного варианта ЕГЭ 2017

24 апреля в 16:00

Комбинированные неравенства

26 апреля в 16:00

Задачи с параметром

15 мая в 16:00

Задачи с параметром

17 мая в 16:00

Задачи с параметром

22 мая в 16:00

Задачи с параметром

24 мая в 18:00

Разбор ЕГЭ

119334, г. Москва,
Ленинский пр-т, 32а

Пн. – Пт.
10.00 – 20.00

Технические требования

Юридическая информация

Партнерская программа

Договор оферты

facebook vk

ok instagram

Пишите нам:

contact@academiarf.ru

Федеральная программа онлайн-обучения для школьников: возможность получить образование столичного уровня в регионах России.

Формула проекта разработана в лаборатории Mitlabs © 2019. Все права защищены.