
Ленинский пр-т, 32а
Пусть даны два уравнения:
1. \(f(x)=0\)
2. \(g(x)=0\)
Уравнения 1 и 2 называются равносильными, если каждое решение уравнения 1 является решением уравнения 2 и, наоборот. Иными словами, два уравнения равносильны, если множество их решений совпадают.
Примеры равносильных преобразований
Возведение уравнения (неравенства) в нечетную натуральную степень (извлечение алгебраического корня нечетной степени) приводит к равносильному уравнению (неравенству).
Если функции \(f(x)\) и \(g(x)\) неотрицательны на некотором множестве, то на этом множестве возведение в четную степень и извлечение арифметического квадратного корня.
Если функция \(h(x)\) определена на \(ОДЗ\) исходного уравнения (неравенства) , то ее можно прибавить (вычесть)у обеим частям уравнения (неравенства).
Если функция \(h(x)\) определена и не обращается в нуль на \(ОДЗ\) исходного уравнения, то обе части уравнения можно одновременно умножить (делить) на эту функцию.
Формулы сокращённого умножения
\((a-b)(a+b) = a^2-b^2\)
\((a\pm b)^2 = a^2\pm 2ab+b^2\)
\(a^3\pm b^3 = (a\pm b)(a^2\mp ab+b^2)\)
\((a\pm b)^3 = 3a^3\pm 3a^2b+3ab^2 \pm b^3\)
Разложение на множители квадратного трёхчлена
Если \(x_1\) и \(x_2\) – корни уравнения \(ax^2+bx+c=0\), то
\(ax^2+bx+c=a(x-x_1)(x-x_2)\)
Свойства степеней:
Возвести число в степень \(n\) - значит умножить его на себя \(n\) раз:
\(a^n=\underbrace{a...a}_{n}\)
При этом \(a^0=1\)
\(a^n\cdot a^m = a^{n+m}\)
\({a^n\over a^m} = a^{n-m}\)
\((a^n)^m=a^{n\cdot m}\)
\((ab)^n=a^n\cdot b^n\)
\({({a\over b})}^n = {a^n\over b^n}\)
\(a^{-n}={1\over a^n}\)
\(a^{m\over n} = {\sqrt[n]{a^m}}\)
Модуль числа
Модуль числа – это расстояние от числа до нуля.
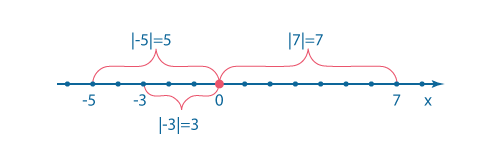
\(|b|=b\), если \(b\) – положительное число.
\(|a|=a\), если \(a\) – отрицательное число.
Алгебраическое определение модуля: \(|a|=\begin {cases} a, \quad a \geq 0 \\ -a, \quad a<0 \end {cases}\)
Корень числа
\(\sqrt[n]a = b\), если \(a=b^n\)
Корень чётной степени можно найти только из неотрицательного числа!
Результат вычисления корня чётной степени тоже всегда неотрицателен по определению!
Если корень нечётной степени, то \(a\) и \(b\) – любые числа.
Свойства корней:
\(\sqrt {ab} = \sqrt a \cdot \sqrt b \)
\(\sqrt {a\over b} = {\sqrt a \over \sqrt b}\)
\((\sqrt[n] a)^n = a\)
\(\sqrt[2n+1] {a^{2n+1}} = |a|\)
\(\sqrt[2n] {a^{2n}} = |a|\)
Дробно-рациональные уравнения – это уравнения, которые содержат алгебраические дроби.
Решение таких уравнений заключается в приведении к дроби вида \({P\over Q} = 0\) где \(P\) и \(Q\) – многочлены.
Алгоритм решения дробно-рациональных уравнений:
1. Привести к одной дроби в левой части и к нулю в правой;
2.Приравнять числитель к нулю;
3. Найти, когда знаменатель превращается в ноль;
4. Выборка ответа.
Существует частный случай решения дробно-рациональных уравнений.
Если дано уравнение, когда дробь равна другой дроби, можно воспользоваться свойством пропорции:
\({P\over Q}={T\over D} \Rightarrow P\cdot D=T \cdot Q\)
Уравнение с одной переменной называют иррациональным, если хотя бы одна из функций или содержит переменную под знаком радикала.
При решении иррациональных уравнений необходимо установить область допустимых значений переменных, исходя из условия, что все радикалы, входящие в уравнение, должны быть арифметическими.
Логарифмы
Логарифм числа \(b\) по основанию \(a\) - это показатель степени, в которую надо возвести число \(a\), чтобы получить число \(b\).
\(y = \log_ax\Leftrightarrow a^y=x\)
Свойства логарифмов:
Основное логарифмическое тождество \(a^{\log_ax}=x\), \(x>0\), \(a>0\), \(a\neq1\)
\( \log_aa=1\), \(a>0\), \(a\neq1\)
\( \log_a1=0\), \(a>0\), \(a \neq 1\)
\(\log_a(bc)=\log_ab+\log_ac\)
\(\log_a{b\over c} = \log_ab - \log_ac\)
\(\log_ab^p=p\log_ab\)
\(\log_{a^k}b={1\over k}\log_ab\)
\(\log_ab= {1\over \log_ba}\)
\(\log_ab={\log_cb\over \log_ca}\)
Тригонометрические уравнения
Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
Простейшие тригонометрические уравнения
\(\sin{x}=a\)
1. \(\sin{x}=0;\) \(x= \pi k.\)
2. \(\sin{x}=1;\) \(x={\pi \over 2} + 2\pi k.\)
3. \(\sin{x}=-1;\) \(x=-{\pi \over 2} + 2\pi k.\)
4. \(\sin{x}=a;\) \(|a|>1\) - решений нет
5. \(\sin{x}=a;\) \(|a|\leq1,\) \(x=(-1)^k \cdot arcsina+ \pi k\)
\(\cos{x}=a\)
1. \(\cos{x}=0;\) \(x={\pi \over 2} + \pi k.\)
2. \(\cos{x}=1;\) \(x=2\pi k.\)
3. \(\cos{x}=-1;\) \(x=\pi + 2\pi k.\)
4. \(\cos{x}=a;\) \(|a|>1\) - решений нет
5. \(\cos{x}=a;\) \(|a|\leq1,\) \(x=\pm arccosa+ 2\pi k\)
\(tgx=a\)
1. \(tgx=0;\) \(x=\pi k.\)
2. \(tgx=a;\) \(x=arctga+ \pi k\)
\(ctgx=a\)
1. \(ctgx=0;\) \(x={\pi \over 2} + 2\pi k.\)
2. \(ctgx=a;\) \(x=arcctga+ \pi k\)
Методы решения тригонометрических уравнений
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше) и решение полученного простейшего тригонометрического уравнения.
Существует семь основных методов решения тригонометрических уравнений:
1. Замена переменной и подстановка
2. Разложение на множители
3. Приведение к однородному уравнению
Уравнение называется однородным относительно \(\sin\) и \(\cos\), если все его члены одной и той же степени относительно \(\sin\) и \(\cos\) одного и того же угла.
Чтобы решить однородное уравнение, надо:
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на \(\cos\) (или \(\sin\)) в старшей степени;
д) решить полученное алгебраическое уравнение относительно \(tg\).
4. Переход к половинному углу
5. Введение вспомогательного угла
6. Преобразование произведения в сумму
7. Универсальная подстановка