| Декартовы координаты на плоскости |
 |
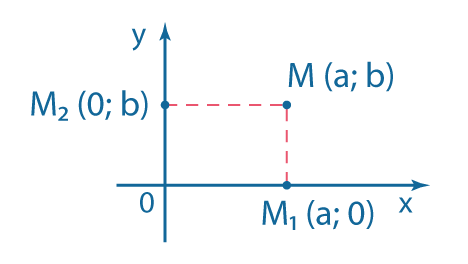\(0\) - начало координат;
\(0x\) - ось абсцисс;
\(0y\) - ось ординат.
|
Расстояние между двумя точками (длина отрезка):
\(d=M_1M_2= \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \)
Деление отрезка в отношении \(\lambda\):
\(x = {x_1+\lambda x_2\over 1+\lambda}\) \(y= {y_1+\lambda y_2\over 1+\lambda}\)
Деление отрезка пополам:
\(x = {x_1+ x_2\over2}\) \(y = {y_1+ y_2\over2}\)
Вектором называется направленный отрезок \(\overrightarrow{AB}\), где точка \(A\) - начало, точка \(B\) - конец вектора.
Нулевым вектором \(\overrightarrow{o}\) называется вектор, у которого начало совпадает с концом.
Векторы \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) называются одинаково направленными или сонаправленными, если лучи \(AB\) и \(CD\) одинаково направлены.
Если лучи \(AB\) и \(CD\) противоположно направлены, векторы \(\overrightarrow{AB}\) и \(\overrightarrow{CD}\) называются противоположно направленными.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора \(\overrightarrow{a}\) обозначают \(|\overrightarrow{a}|\).
Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине.
Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными. Вектор, противоположный вектору \(a\), обозначается как \(-\overrightarrow{a}\).
Сложение векторов
Сложение векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу треугольника:
Суммой \(\overrightarrow{a} +\overrightarrow{b}\) двух векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) называют такой третий вектор \(\overrightarrow{c}\), начало которого совпадает с началом \(\overrightarrow{a}\), а конец - с концом \(\overrightarrow{b}\) при условии, что конец вектора \(\overrightarrow{a}\) и начало вектора \(\overrightarrow{b}\) совпадают.
Сложение векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу параллелограмма:
Если два неколлинеарных вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\) привести к общему началу, то вектор \(\overrightarrow{c}=\overrightarrow{a} +\overrightarrow{b}\) совпадает с диагональю параллелограмма, построенного на векторах \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Причем начало вектора \(\overrightarrow{c}\) совпадает с началом заданных векторов.
Разностью \(\overrightarrow{a} -\overrightarrow{b}\) векторов называется вектор \(\overrightarrow{c}\) такой, что выполняется условие:
\(\overrightarrow{b} +\overrightarrow{c}=\overrightarrow{a}\).
Координаты вектора
Пусть вектор \(\overrightarrow{a}\) имеет началом точку \(A_1(x_1;y_1)\), а концом - точку \(A_2(x_2;y_2)\).
Координатами вектора \(\overrightarrow{a}\) называются числа \(a_1=x_2-x_1,~a_2=y_2-y_1\). Обозначают так: \(\overrightarrow{a}(a_1;a_2)\).
Координаты нулевого вектора равны нулю.
Длина вектора (или абсолютная величина вектора) \(\overrightarrow{a}(a_1;a_2)\) выражается формулой
\(|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2}\)
Равные векторы имеют равные соответствующие координаты.
И наоборот. Если у векторов соответствующие координаты равны, то векторы равны.
Сложение векторов
Суммой векторов \(\overrightarrow{a}(a_1;a_2)\) и \(\overrightarrow{b}(b_1;b_2)\) называется вектор \(\overrightarrow{c}\) с координатами \((a_1+b_1, a_2+b_2)\).
Умножение вектора на число
Произведением вектора \(\overrightarrow{(a_1;a_2)}\) на число \(\lambda\) называется вектор \(\overrightarrow{(\lambda a_1;\lambda a_2)}\), то есть
\(\lambda\overrightarrow{(a_1;a_2)} = \overrightarrow{(\lambda a_1;\lambda a_2)}\)
Коллинеарные вектора
Пусть \(\overrightarrow{a}\) и \(\overrightarrow{b}\) - отличные от нуля коллинеарные векторы. Тогда существует число \(\lambda\) такое, что \(\overrightarrow{b}=\lambda\overrightarrow{a}\)
Угол между векторами
Углом между любыми двумя ненулевыми векторами \(\overrightarrow{a}\) и \(\overrightarrow{b}\) называется угол между равными им векторами с общим началом (наименьший угол).
 |
⇒
|
|
Угол между двумя векторами находится в промежутке [0°; 180°].
Угол между одинаково направленными векторами равен нулю.
Скалярное произведение векторов
- Скалярным произведением векторов \(\overrightarrow{a}(a_1;a_2)\) и \(\overrightarrow{b}(b_1;b_2)\) называется число \(a_1b_1+a_2b_2\), то есть:
\(\overrightarrow{a} \cdot \overrightarrow{b}=a_1b_1+a_2b_2\)
- Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними, то есть:
\(\overrightarrow{a} \cdot \overrightarrow{b}=|\overrightarrow{a}| \cdot |\overrightarrow{b}|\cdot cos ∠(\overrightarrow{a}; \overrightarrow{b})\)
Следовательно, если векторы перпендикулярны, то их скалярное произведение равно нулю. Верно и обратное.
Из формул I и II скалярного произведения вытекает, что угол между векторами можно найти, используя формулу:
\(cos ∠(\overrightarrow{a}; \overrightarrow{b})={\overrightarrow{a} \cdot \overrightarrow{b} \over{|\overrightarrow{a}| \cdot |\overrightarrow{b}|}}= {a_1b_1+a_2b_2\over{ \sqrt {a_1^2+a_2^2}\sqrt {b_1^2+b_2^2}}}\)
Также, следствием, например, формулы II скалярного произведения есть следующий важный момент:
\(\overrightarrow{a}^2=|\overrightarrow{a}|^2\)
Функции и их свойства
Функция — одно из важнейших математических понятий. Функцией называют такую зависимость переменной \(y\) от переменной \(x\), при которой каждому значению переменной \(x\) соответствует единственное значение переменной \(y\).
Переменную \(x\) называют независимой переменной или аргументом. Переменную \(y\) называют зависимой переменной. Говорят также, что переменная \(y\) является функцией от переменной \(x\). Значения зависимой переменной называют значениями функции.
Если зависимость переменной \(y\) от переменной \(x\) является функцией, то коротко это записывают так: \(y=f(x)\). (Читают: \(y\) равно \(f\) от \(x\).) Символом \(f(x)\) обозначают значение функции, соответствующее значению аргумента, равному \(x\).
Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Способы задания функции:
1. аналитический способ (функция задается с помощью математической формулы);
2. табличный способ (функция задается с помощью таблицы);
3. описательный способ (функция задается словесным описанием);
4. графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Основные свойства функций:
1. Нули функции
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
2. Промежутки знакопостоянства функции
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
3. Возрастание (убывание) функции
Возрастающая в некотором промежутке функция - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая в некотором промежутке функция - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
4. Четность (нечетность) функции
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого \(x\) из области определения выполняется равенство \(f(-x) = f(x)\). График четной функции симметричен относительно оси ординат.
Например, \(y=x^2\) - четная функция.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство \( f(-x) = - f(x)\). График нечетной функции симметричен относительно начала координат.
Например: \(y=x^3\) - нечетная функция.
Функция общего вида не является четной или нечетной \((y=x^{2}+x)\).
