«Академия»

О нас Об academiaRF.ru СМИ о нас Полезная информация Юридическая информация Курсы ОГЭ ЕГЭ Годовые курсы Экспресс-подготовка Русский язык Математика Обществознание Английский язык Лекции для родителей Преподаватели Косицына Евгения Федоровна Алексеева Вера Олеговна Бородкина Ольга Викторовна Новичкова Дана Александровна Филимонова Елена Викторовна Макарова Галина Юрьевна Раскина Дина Анатольевна Музычка Андрей Юрьевич Расписание Сегодня Неделя Месяц Тесты Русский язык. ЕГЭ Русский язык. ОГЭ Математика. ЕГЭ Математика. ОГЭ Физика. ЕГЭ Обществознание. ЕГЭ Английский язык. B1 Досрочный ЕГЭ по математике 2017 Разбор Демо 2017 Русский язык Разбор Демо 2017 Математика Разбор Демо 2017 Обществознание Разбор Демо 2017 Английский язык Стоимость

Регистрация Вход

Бесплатно. ОГЭ. Математика. Годовой курс 22 урока, 44 часа

Числа и вычисления

Бесплатный

Числа, действия с числами. Измерения, приближения, оценки

Алгебраические выражения и уравнения

Бесплатный

Преобразования алгебраических дробей

Бесплатный

Многочлены

Бесплатный

Уравнения

Бесплатный

Рациональные и иррациональные выражения и уравнения

Неравенства

Бесплатный

Неравенства

Числовые последовательности

Бесплатный

Арифметическая и геометрическая прогрессии

Реальная математика

Бесплатный

Текстовые задачи. Базовый уровень

Бесплатный

Текстовые задачи. Повышенный уровень

Бесплатный

Вероятность. Комбинаторика

Бесплатный

Экономические задачи. Статистика

Координаты и функции

Бесплатный

Координатная прямая. Координатная плоскость

Бесплатный

Координатная плоскость. Векторы. Линейная функция

Бесплатный

Числовые функции, графики, геометрический смысл коэффициентов

Геометрия

15.02.17 18:00

Урок 15

Бесплатный

Измерение геометрических величин. Углы. Расстояния. Треугольники

Бесплатный

Треугольник

Бесплатный

Четырехугольники

Бесплатный

Четырехугольники. Многоугольники

Бесплатный

Окружность и круг

Бесплатный

Комбинация многоугольников и окружностей

Разбор ОГЭ

Бесплатный

Разбор ОГЭ

Бесплатный

Разбор ОГЭ

Урок 15. Измерение геометрических величин. Углы. Расстояния. Треугольники

Геометрические фигуры и смежные углы

Урок завершен 15 февраля в 18:00

Записаться на открытый урок

Измерение геометрических величин. Угол. Прямой угол. Острые и тупые углы. Расстояния.

Урок

Смотреть запись урока

Теория

Прямые углы на плоскости

Виды углов

Острый угол
\(0°< \alpha<90°\)

Прямой угол
\(\alpha=90°\)

Тупой угол
\(90°< \alpha<180°\)

Развёрнутый угол
\(\alpha=180°\)

Вертикальные углы равны

Смежные углы составляют в сумме 180°:
\(\alpha + \beta= 180°\)

Углы с соответственно параллельными сторонами

Либо равны,

либо составляют в сумме 180°

Углы с соответственно параллельными сторонами

Либо равны,

либо составляют в сумме 180°

Параллельные прямые

Так называются прямые, которые не перессекаются.

Признаки и свойства параллельных прямых

Внутренние накрест лежащие углы равны

Сумма внутренних односторонних углов равна 180°

Внешние накрест лежащие
углы равны

Сумма внешних односторонних углов равна 180°

Соответственные углы равны

Соотношения между сторонами и углами в прямоугольном треугольнике

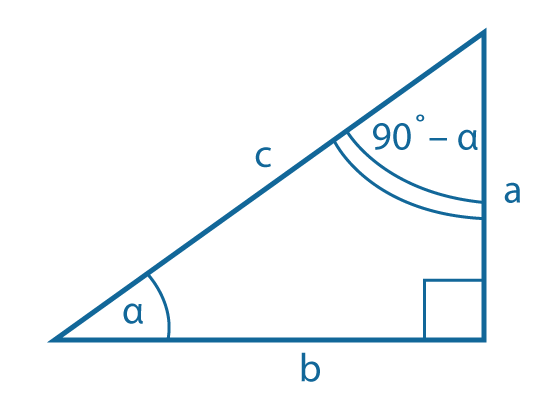\({a \over c }=sin~ α=cos(90°-α)\)

\({b \over c }=cos~ α=sin(90°-α)\)

\({a \over b }=tg~ α=ctg(90°-α)\)

\({b \over a }=ctg~ α=tg(90°-α)\)

Площадь треугольника

	Через сторону и высоту, проведенную к ней: \(S={1 \over2}ah_a\)
	Через две стороны и угол между ними: \(S={1 \over2}ab ~sin \gamma\)
	Формула Герона Через три стороны: \(S= \sqrt {p(p-a)(p-b)(p-c)}\), где \(p={a+b+с \over 2}\)
	Через полупериметр и радиус вписанной окружности: \(S=pr\), где \(p={a+b+с \over2}\).
	Через произведение сторон и радиус описанной окружности: \(S={abc\over4R}\)

Площадь прямоугольного треугольника

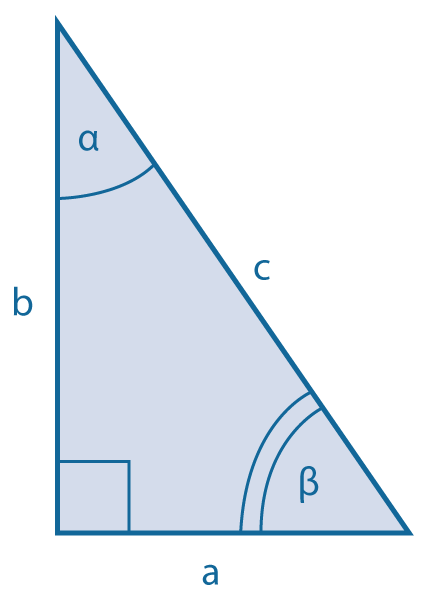Через катеты: \(S={1\over2}ab\)

Через катет и острый угол:
\(S={1\over2}a^2tgβ={1\over2}a^2ctgα\)

Через гипотенузу и любой из острых углов:
\(S={1\over4}c^2sin~2α={1\over4}c^2sin~2β\)

Площадь круга и его частей

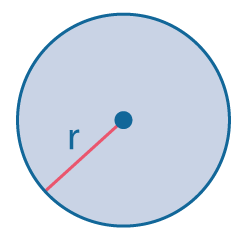	Площадь круга: \(S=pr^2\)
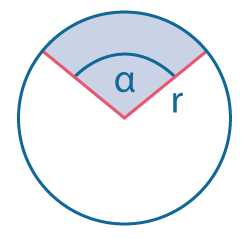	Площадь сектора: \(S={1\over 2}αr^2\) (угол \(α\) в радианах).
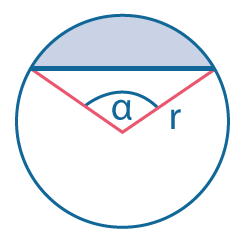	Площадь сегмента: \(S={1\over 2}(α-sin~α)r^2\) (угол \(α\) в радианах).

Площадь трапеции

Через полусумму оснований и высоту:

\(S = {a+b \over 2}h\)

Через среднюю линию и высоту:

\(S=MN \cdot h\)

Через диагонали и угол между ними:

\(S={d_1d_2~sin \varphi \over 2}\)

Методические материалы к уроку

Для того, чтобы открыть методический материал, необходимо записаться на урок.

Практикум

Для прохождения домашнего задания, вам необходимо записаться на урок.

Филимонова Елена Викторовна

подробнее о преподавателе

19 октября в 18:00

Числа, действия с числами. Измерения, приближения, оценки

2 ноября в 18:00

Преобразования алгебраических дробей

9 ноября в 18:00

Многочлены

16 ноября в 18:00

Уравнения

23 ноября в 18:00

Рациональные и иррациональные выражения и уравнения

30 ноября в 18:00

Неравенства

7 декабря в 18:00

Арифметическая и геометрическая прогрессии

14 декабря в 18:00

Текстовые задачи. Базовый уровень

21 декабря в 18:00

Текстовые задачи. Повышенный уровень

11 января в 18:00

Вероятность. Комбинаторика

18 января в 18:00

Экономические задачи. Статистика

25 января в 18:00

Координатная прямая. Координатная плоскость

1 февраля в 18:00

Координатная плоскость. Векторы. Линейная функция

8 февраля в 18:00

Числовые функции, графики, геометрический смысл коэффициентов

15 февраля в 18:00

Измерение геометрических величин. Углы. Расстояния. Треугольники

22 февраля в 18:00

Треугольник

1 марта в 18:00

Четырехугольники

15 марта в 18:00

Четырехугольники. Многоугольники

22 марта в 18:00

Окружность и круг

29 марта в 18:00

Комбинация многоугольников и окружностей

5 апреля в 18:00

Разбор ОГЭ

12 апреля в 18:00

Разбор ОГЭ

119334, г. Москва,
Ленинский пр-т, 32а

Пн. – Пт.
10.00 – 20.00

Технические требования

Юридическая информация

Партнерская программа

Договор оферты

facebook vk

ok instagram

Пишите нам:

contact@academiarf.ru

Федеральная программа онлайн-обучения для школьников: возможность получить образование столичного уровня в регионах России.

Формула проекта разработана в лаборатории Mitlabs © 2019. Все права защищены.