Треугольники
 |
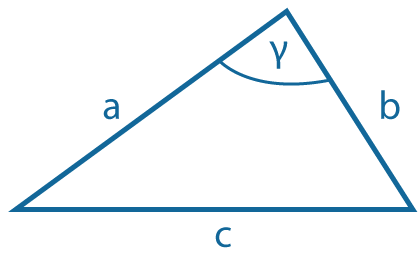Теорема косинусов:
\(c^2=a^2+b^2-2ab~cos γ\)
|
 |
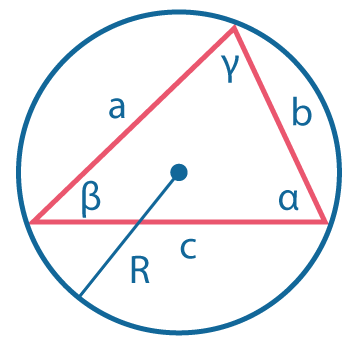Теорема синусов:
\({a \over sin~α}={b \over sin~β}={c \over sin~γ}\).
Это отношение равно \(2R\), где \(R\) - радиус описанной окружности.
|
Свойства биссектрис
 |
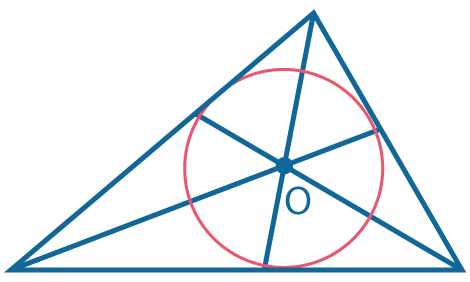Три биссектрисы пересекаются в одной точке, которая всегда лежит внутри треугольника.
Эта точка является центром вписанной окружности.
|
 |
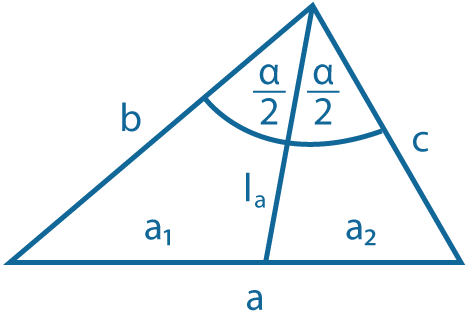Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам:
\( {a_1 \over a_2}= {b \over c}\)
|
Вписанная и описанная окружности
 |
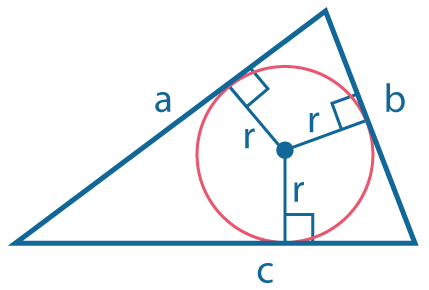В любой треугольник можно вписать окружность.
Центр вписанной окружности - точка пересечения биссектрис.
Радиус вписанной окружности:
\(r=S/p\), где \(S\) - площадь треугольника,
\(p={{a+b+c} \over2}\).
|
 |
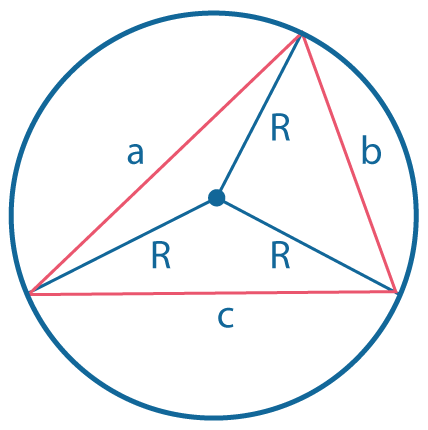Около любого треугольника можно описать окружность.
Центр описанной окружности - точка пересечения серединных перпендикуляров.
Радиус описанной окружности:
\(R= {abc \over 4S}\), где \(S\) - площадь треугольника.
|
Окружность, вписанная в прямоугольный треугольник
 |
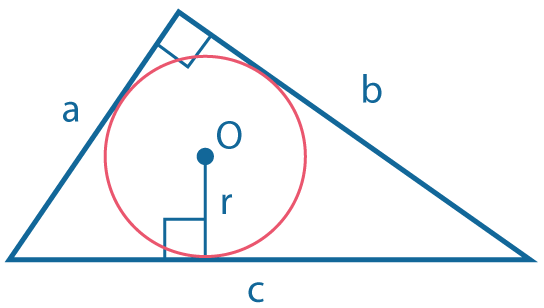Радиус вписанной окружности:
\(r={ab\over a+b+c}\),
\(r={a+b-c\over 2}\).
|
 |
Центр описанной окружности совпадает с серединой гипотенузы, а радиус равен:
- половине гипотенузы:
\(R = {c \over 2}\)
- медиане, проведенной к гипотенузе:
\(R =m_c\)
|
Окружность, описанная около прямоугольника
 |
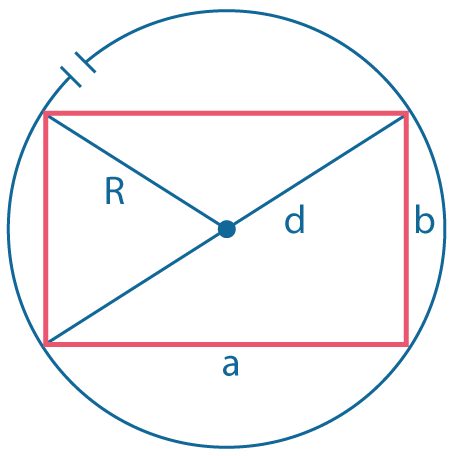Около любого прямоугольника можно описать окружность.
Радиус описанной окружности:
\(R={d \over 2}\),
где \(d= \sqrt {a^2+b^2}\) - диагональ прямоугольника.
|
Окружность, вписанная в ромб
 |
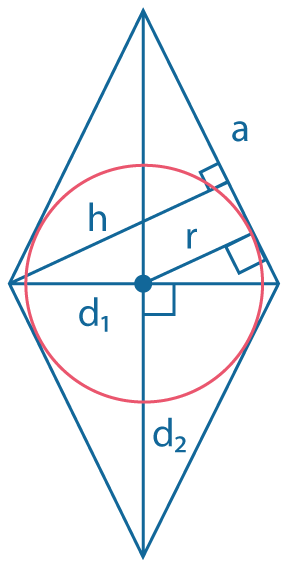В любой ромб можно вписать окружность. Радиус \(r\) вписанной окружности удовлетворяет соотношениям:
\(r={h \over 2}\), где \(h\) - высота ромба,
\(r={d_1d_2 \over 4a}\), где \(d_1 ~и ~d_2\) - диагонали ромба, \(a\) - его сторона
|
 |
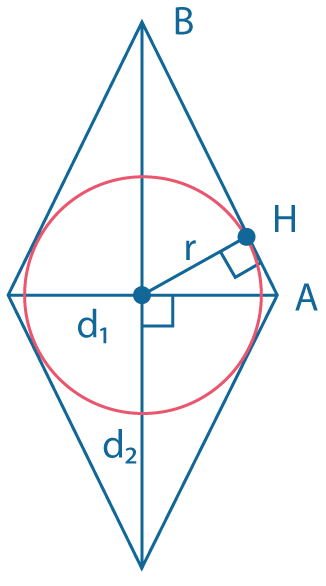Точка касания вписанной окружности делит сторону ромба на отрезки, связанные с его диагоналями и радиусом вписанной окружности следующими соотношениями:
\(d_1=2 \sqrt{AH \cdot AB}\)
\(d_2=2 \sqrt{BH \cdot AB}\)
\(r= \sqrt{AH \cdot HB}\)
|
Площадь ромба
 |
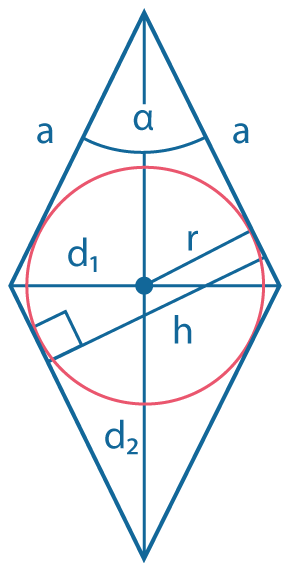Через сторону и высоту: \(S = ah\)
Через сторону и радиус вписанной окружности: \(S = 2ar\)
Через сторону и угол ромба: \(S=a^2sin~ \alpha\)
Через диагонали: \(S={d_1d_2 \over2}\)
|
Окружность, описанная около квадрата
 |
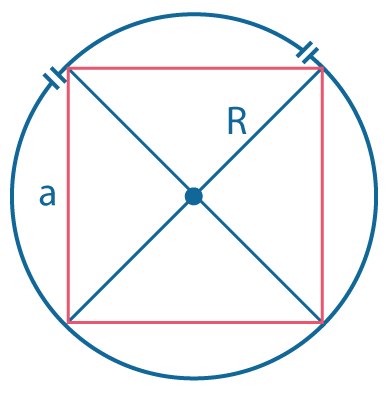Около квадрата можно описать окружность.
Радиус описанной окружности выражается через сторону \(a\) квадрата и его диагональ \(d\) следующим образом:
\(R={a \over \sqrt2}={d \over2}\)
|
Окружность, вписанная в квадрат
 |
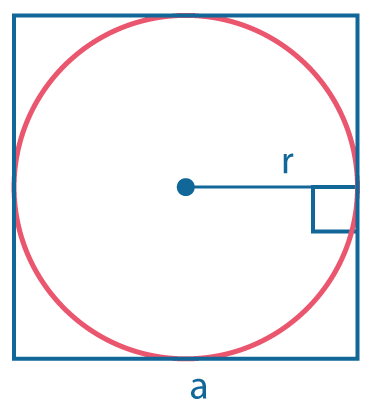В квадрат можно вписать окружность. Радиус вписанной окружности равен половине стороны:
\(r={a\over 2}\)
|
Окружность, описанная и вписанная в трапецию
 |
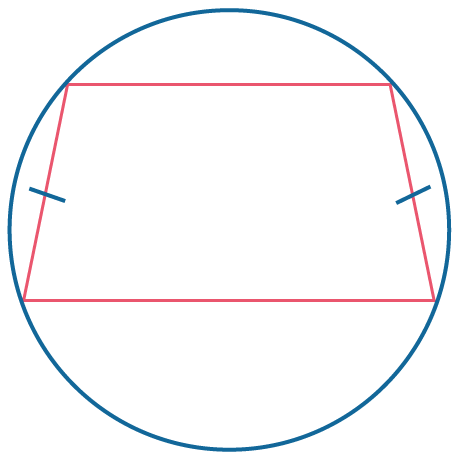Любую равнобокую трапецию можно вписать в окружность.
Вписать в окружность можно только равнобокую трапецию.
|
 |
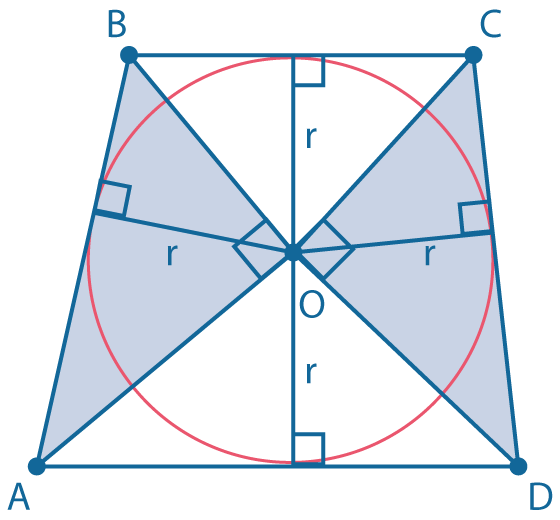Если трапеция \(ABCD\) описана около окружности, то треугольники \(AOB ~и ~DOC\) прямоугольные (точка \(O\) - центр вписанной окружности).
Высоты этих треугольников, опущенные на гипотенузы, равны радиусу вписанной окружности, а высота трапеции равна диаметру вписанной окружности.
|
Четырехугольник, описанный около окружности
 |
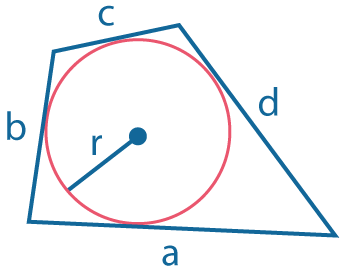Четырехугольник можно описать около окружности, если суммы противолежащих сторон равны:
\(a+b=c+d\)
Если четырехугольник описан около окружности, то суммы противолежащих сторон равны
|
|
Площадь: \(S=pr\), где \(p={a+b+c+d\over 2}\) (полупериметр), \(r\) - радиус вписанной окружности.
Данная формула справедлива для любого многоугольника,
описанного около окружности.
|
Четырехугольник, вписанный в окружность
 |
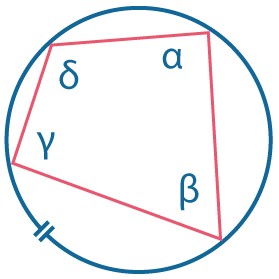Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна 180°:
\(\alpha + \gamma= \beta + \sigma=180°\)
Если четырехугольник вписан в окружность, то суммы противолежащих углов равны 180°.
|
 |
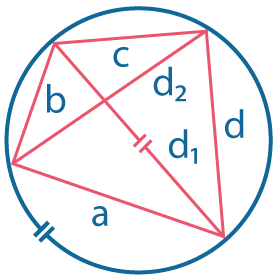Теорема Птолемея
Сумма произведений противолежащих сторон равна произведению диагоналей:
\(ac+bd=d_1d_2\)
|
 |
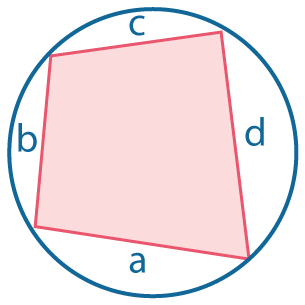Площадь
\(S= {\sqrt {(p-a)(p-b)(p-c)(p-d)}}\), где \(p={a+b+c+d\over 2}\) (полупериметр)
|
