Паралеллограмом называется четурыёхугольник, противоположные стороны которого попарно параллельны.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Ромбом называется параллелограмм, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны. Из определния следует, что квадрат является ромбом, следовательно, он обладает всеми свойствами прямоугольника и ромба.
Трапецией называется четырёхугольник, две стороны которого параллельны, а две другие не параллельны.

Площадь четырёхугольника

Площадь параллелограмма равна произведению его основания на высоту.
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.
Площадь трапеции равна произведению полусуммы её оснований на высоту.
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Свойства параллелограмма

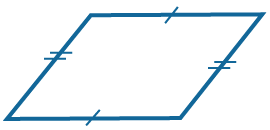	Противолежащие стороны попарно равны.
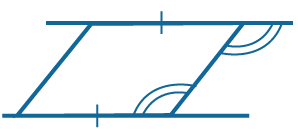	Противолежащие стороны равны и параллельны.
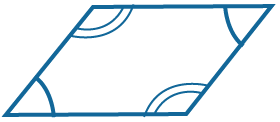	Противолежащие углы попарно равны.
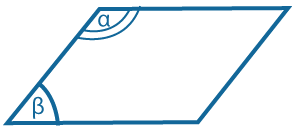	Сумма углов, прилежащих к любой стороне, равна 180°: \(α+ β=180°\)
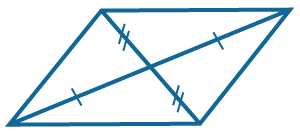	Диагонали точкой пересечения делятся пополам.

Площадь параллелограмма

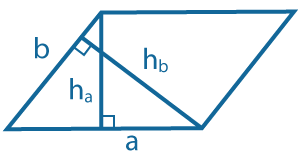Через сторону и опущенную на нее высоту:

\(S=ah_a=bh_b\)

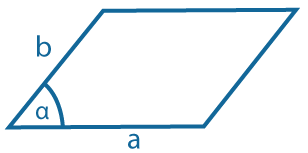Через две прилежащие стороны и угол между ними:

\(S=ab~sin~α\)

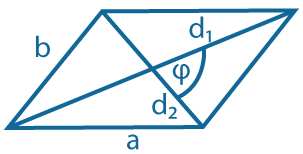Через диагонали и угол между ними:

\(S = {d_1d_2~sin\varphi \over 2}\)

Элементы трапеции

\(a, b\) - основания \((a~||~b)\)
\(m,~n\) - боковые стороны
\(d_1, d_2\) - диагонали

\(h\) - высота (отрезок, соединяющий основания и перпендикулярный им)
\(MN\) - средняя линия (отрезок, соединяющий середины боковых сторон)

Свойства трапеции

Средняя линия параллельна основаниям, равна их полусумме и делит любой отрезок с концами, лежащими на прямых, содержащих основания, (например, высоту трапеции) пополам:

\(MN~||~a, MN~||~b, MN={a+b\over 2}\)