
Ленинский пр-т, 32а
Произвольный треугольник
Соотношения между сторонами и угламми
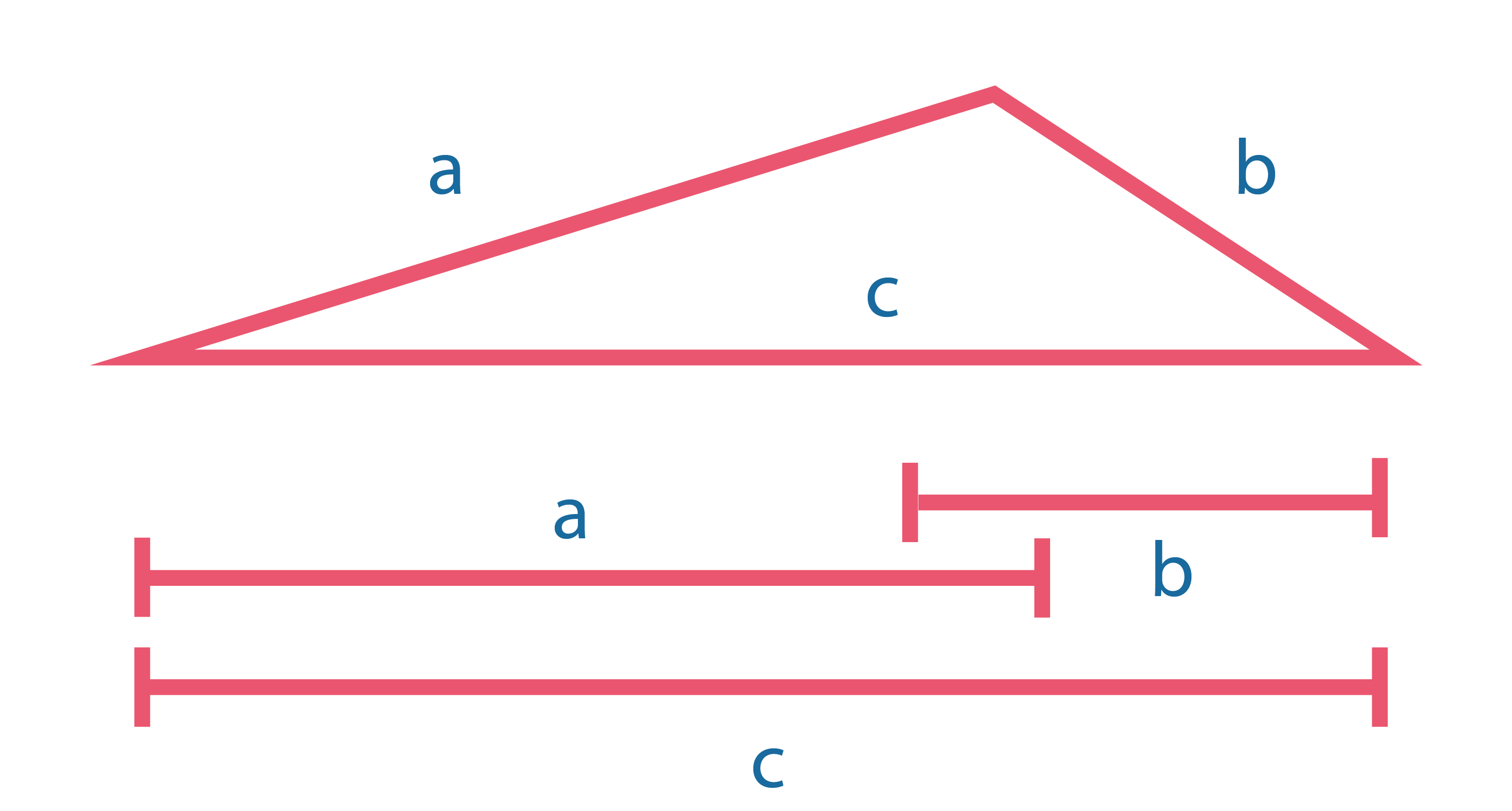 |
Неравенство треугольника Любая сторона треугольника меньше суммы двух других сторон, но больше модуля их разности: \(|a-b| < c < a+b\) |
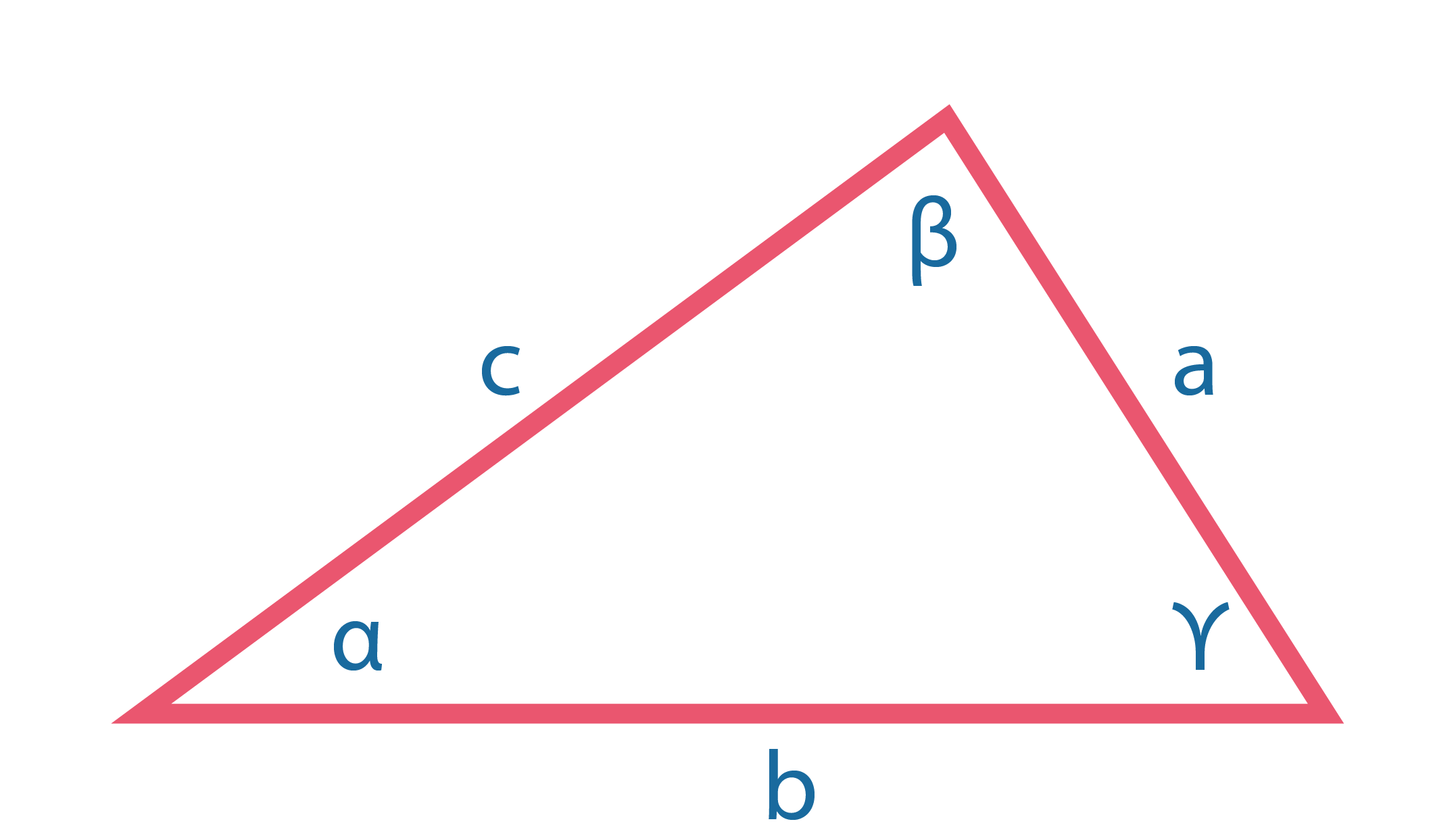 |
Сумма углов треугольника равна 180°: \(\alpha+\beta+\gamma=180°\) Против большей стороны в треугольнике лежит больший угол: \(b>a⇔ \beta> \alpha\) |
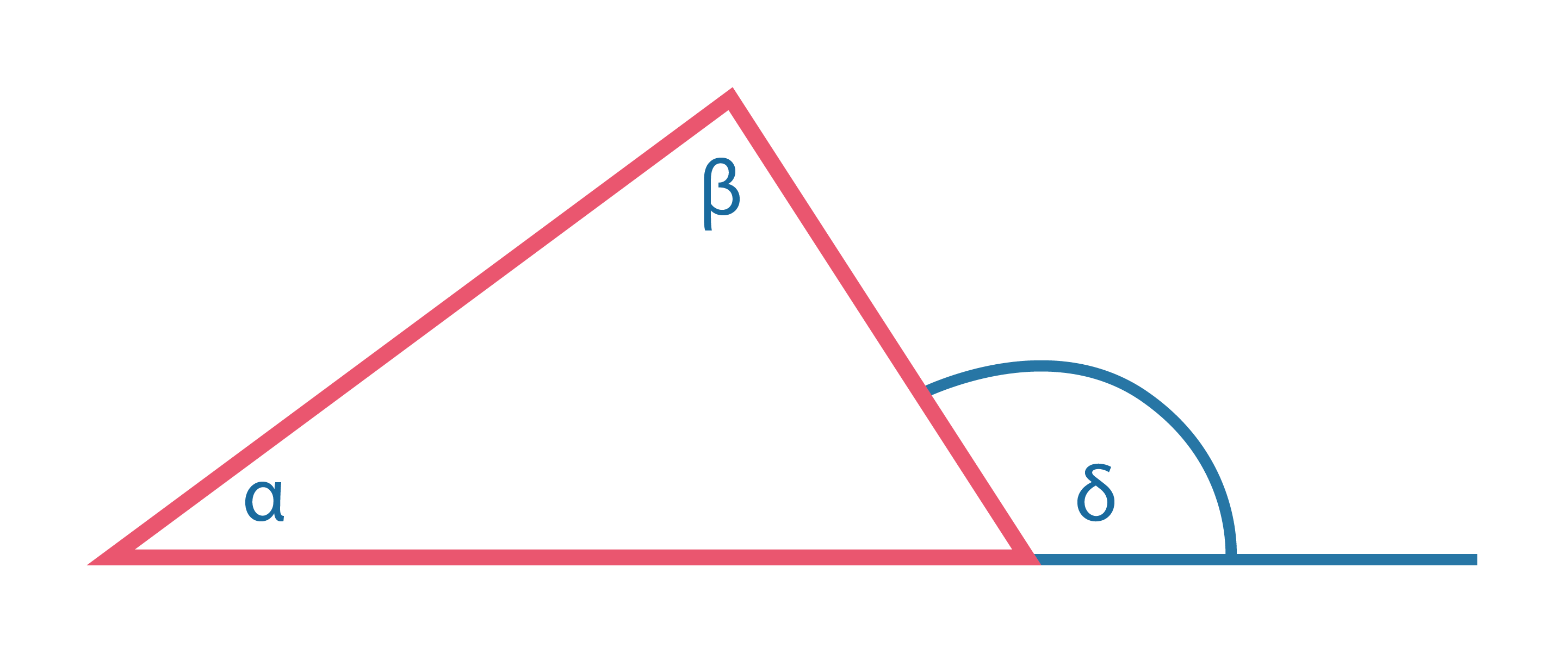 |
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним: \(\sigma= \alpha + \beta\) |
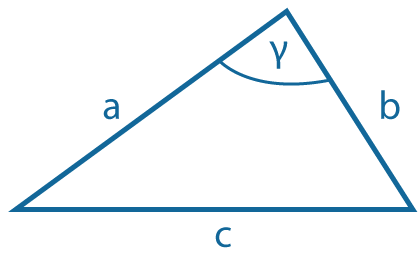 |
Теорема косинусов: \(c^2=a^2+b^2-2ab~cos γ\) |
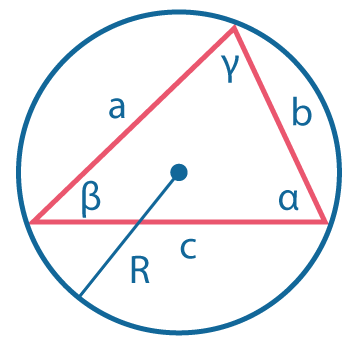 |
Теорема синусов: \({a \over sin~α}={b \over sin~β}={c \over sin~γ}\). Это отношение равно \(2R\), где \(R\) - радиус описанной окружности. |
Признаки равенства треугольников
|
По двум сторонам и углу между ними |
По одной стороне и двум прилежащим к ней углам |
По трем сторонам |
Признаки подобия треугольников
|
По двум пропорциональным сторонам и углу между ними: \({a \over a_1}= {b \over b_1}\) |
По двум равным углам. |
По трем пропорциональным сторонам: \({a \over a_1}= {b \over b_1}= {c \over c_1}\) |
Свойства медиан
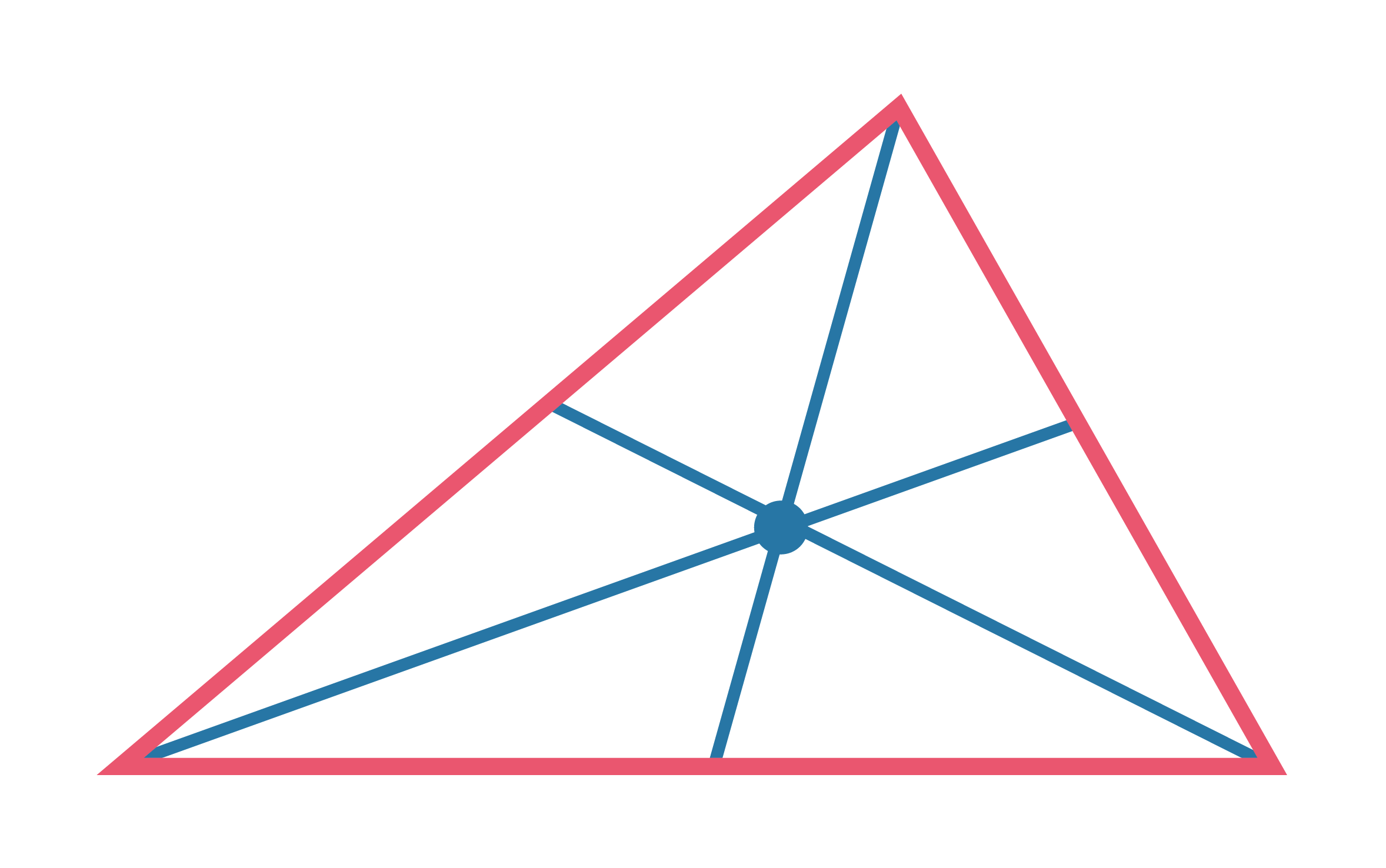 |
Три медианы пересекаются в одной точке, которая всегда находится внутри треугольника (центр масс треугольника). |
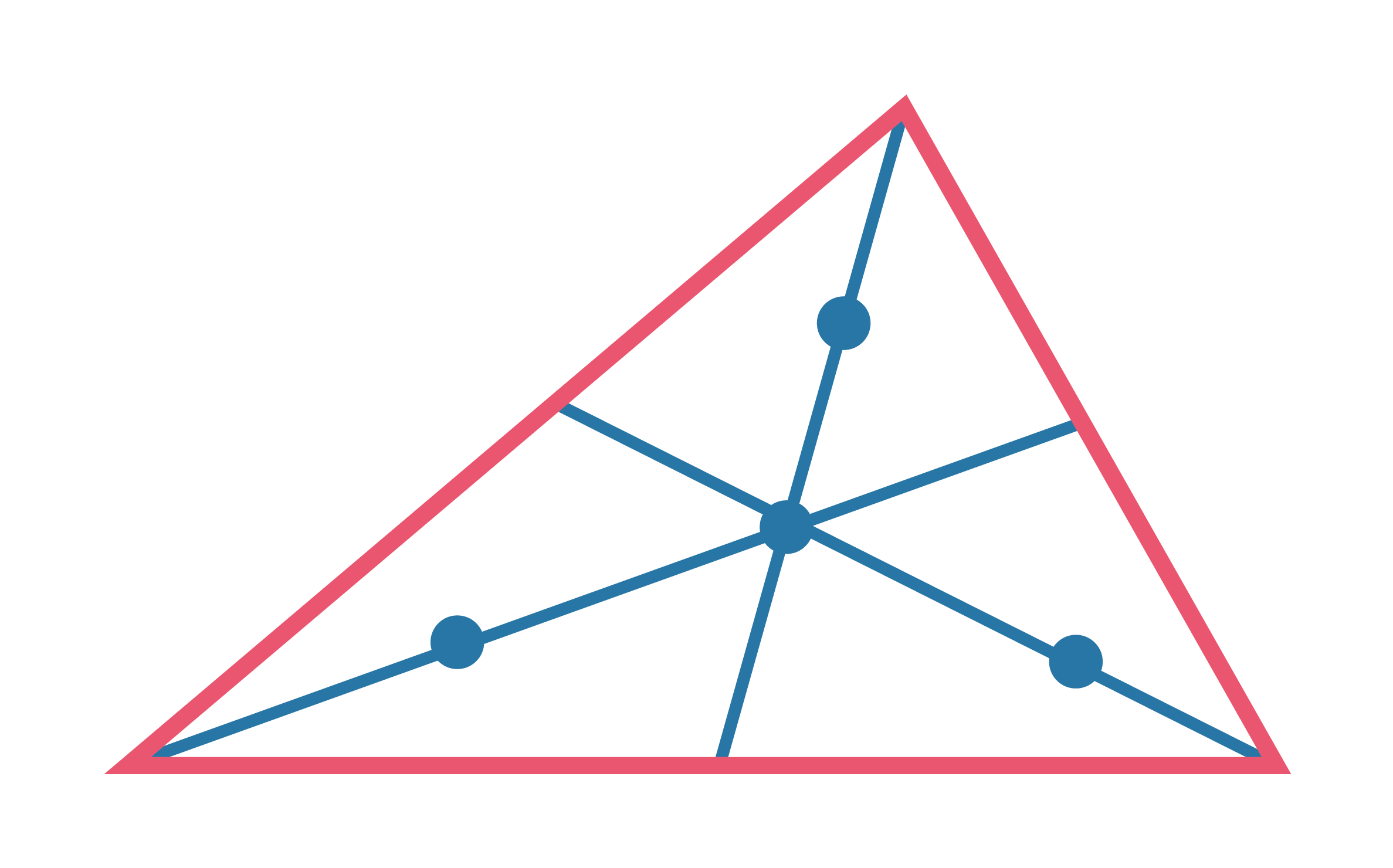 |
Каждая медиана точкой пересечения медиан делится в отношении 2:1, считая от вершины. |
|
Каждая медиана делит треугольник на 2 равновеликих треугольника (одинаковой площади). |
|
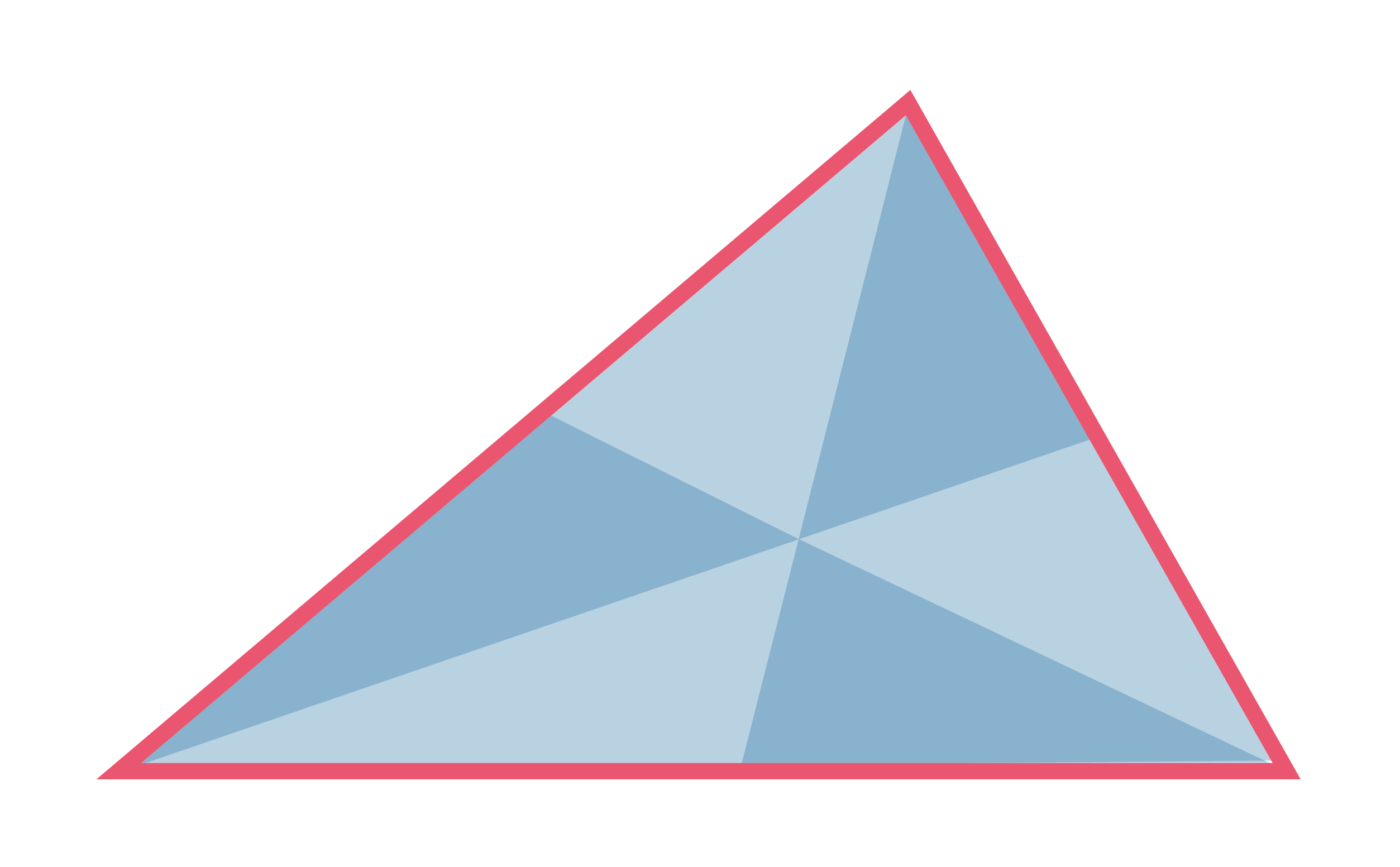 |
Три медианы делят треугольник на 6 равновеликих треугольников. |
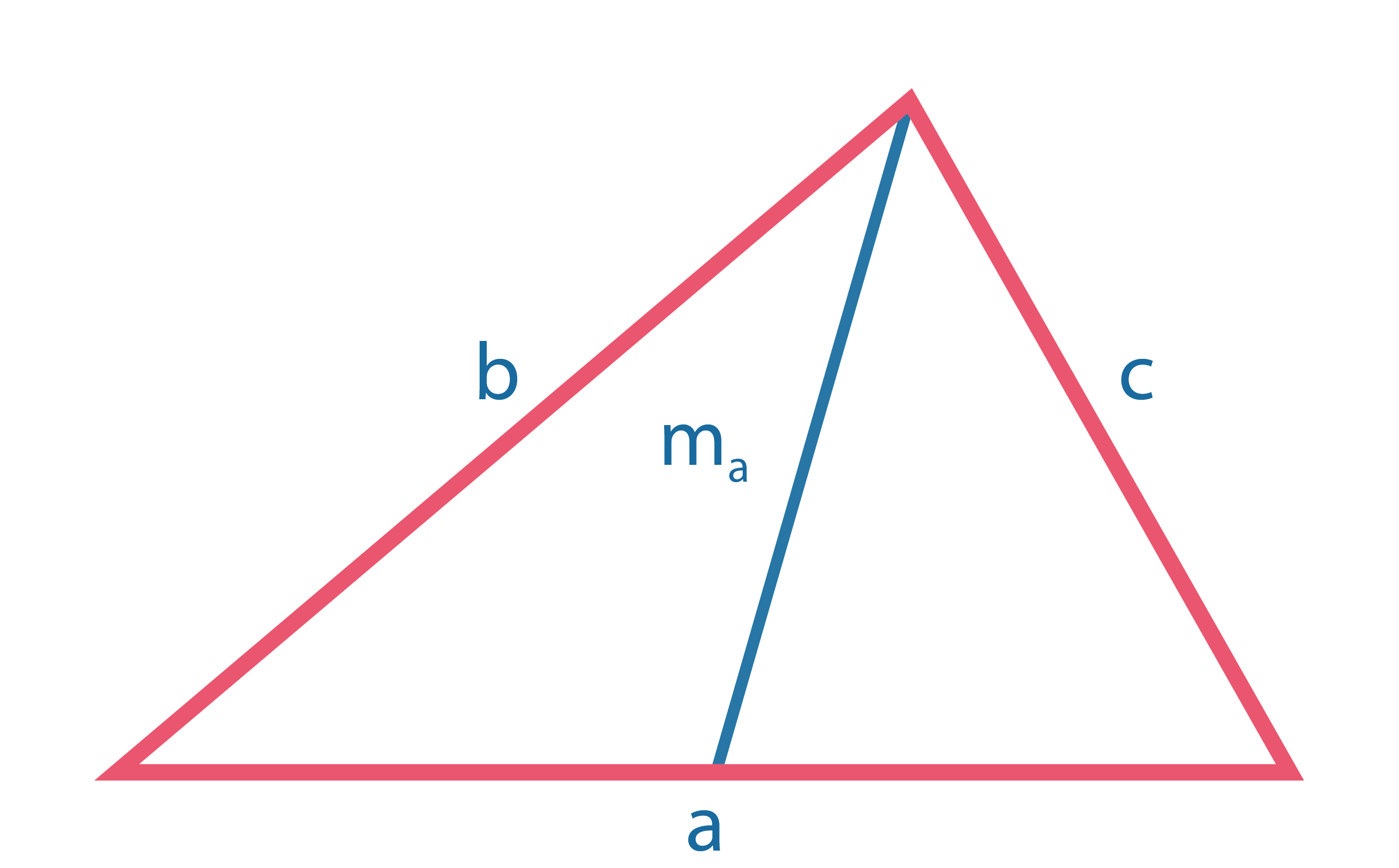 |
Длина медианы \(m_a={1 \over 2} \sqrt{2b^2+2c^2 -a^2}\) |
Свойства биссектрис
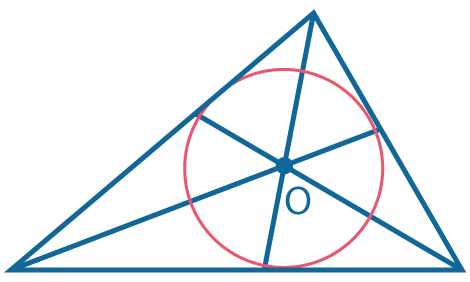 |
Три биссектрисы пересекаются в одной точке, которая всегда лежит внутри треугольника. |
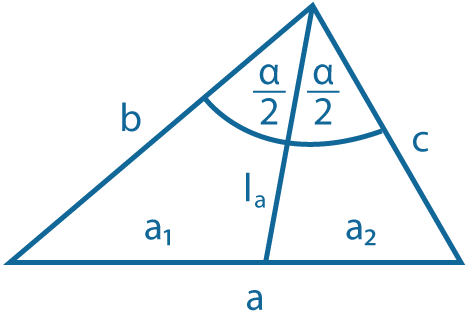 |
Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам: \( {a_1 \over a_2}= {b \over c}\) |
|
Биссектрисы внутреннего и внешнего угла перпендикулярны. |
|
|
|
Длина биссектрисы \(l_a={2bc~cos~ {\alpha \over 2}\over b+c}\) \(l_a^2=bc-b_1c_1\) |
Свойства высот
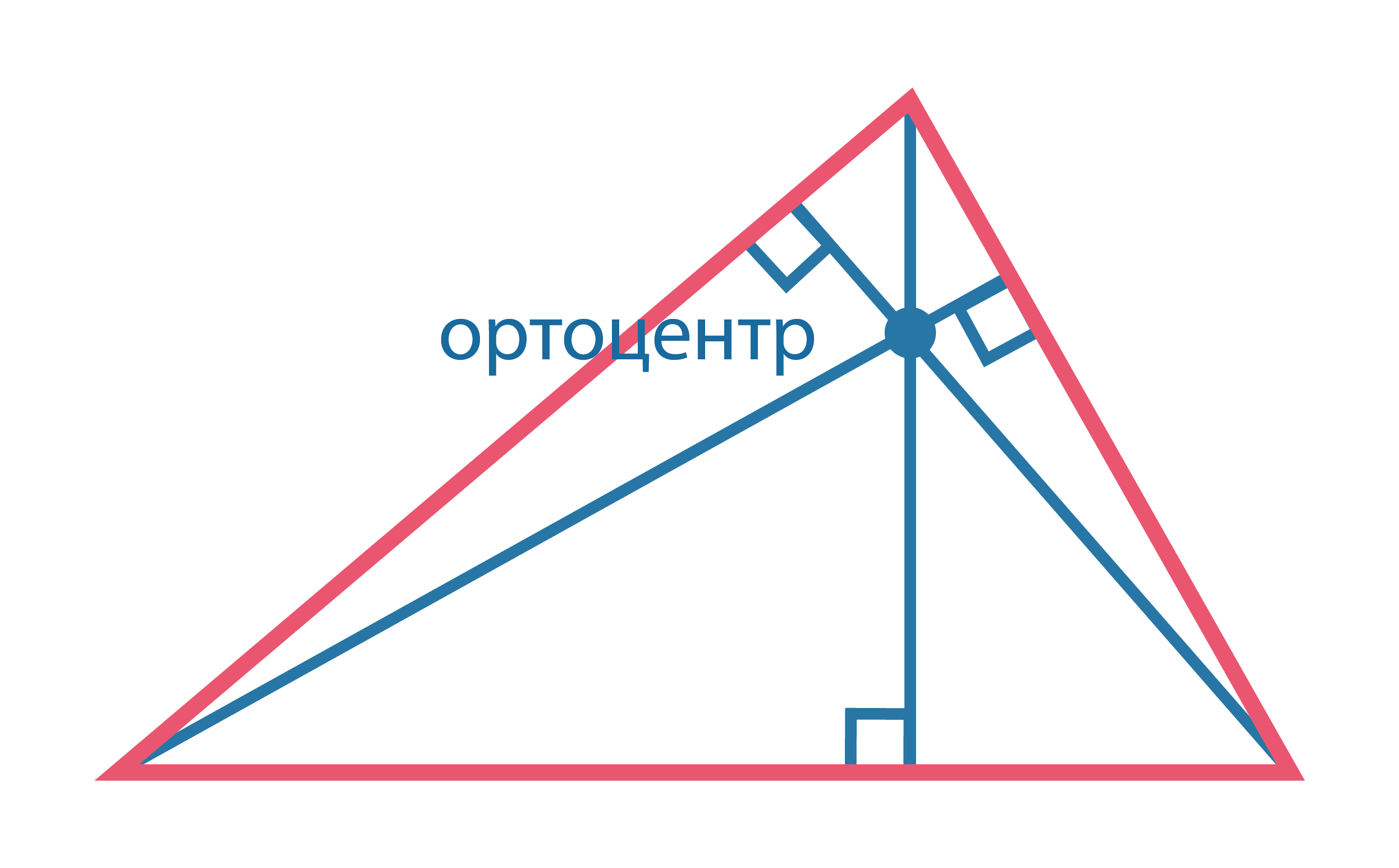 |
Прямые, содержащие высоты треугольника, пересекаются в одной точке. Эта точка называется ортоцентром. Ортоцентр остроугольного треугольника лежит внутри треугольника. |
|
|
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла. |
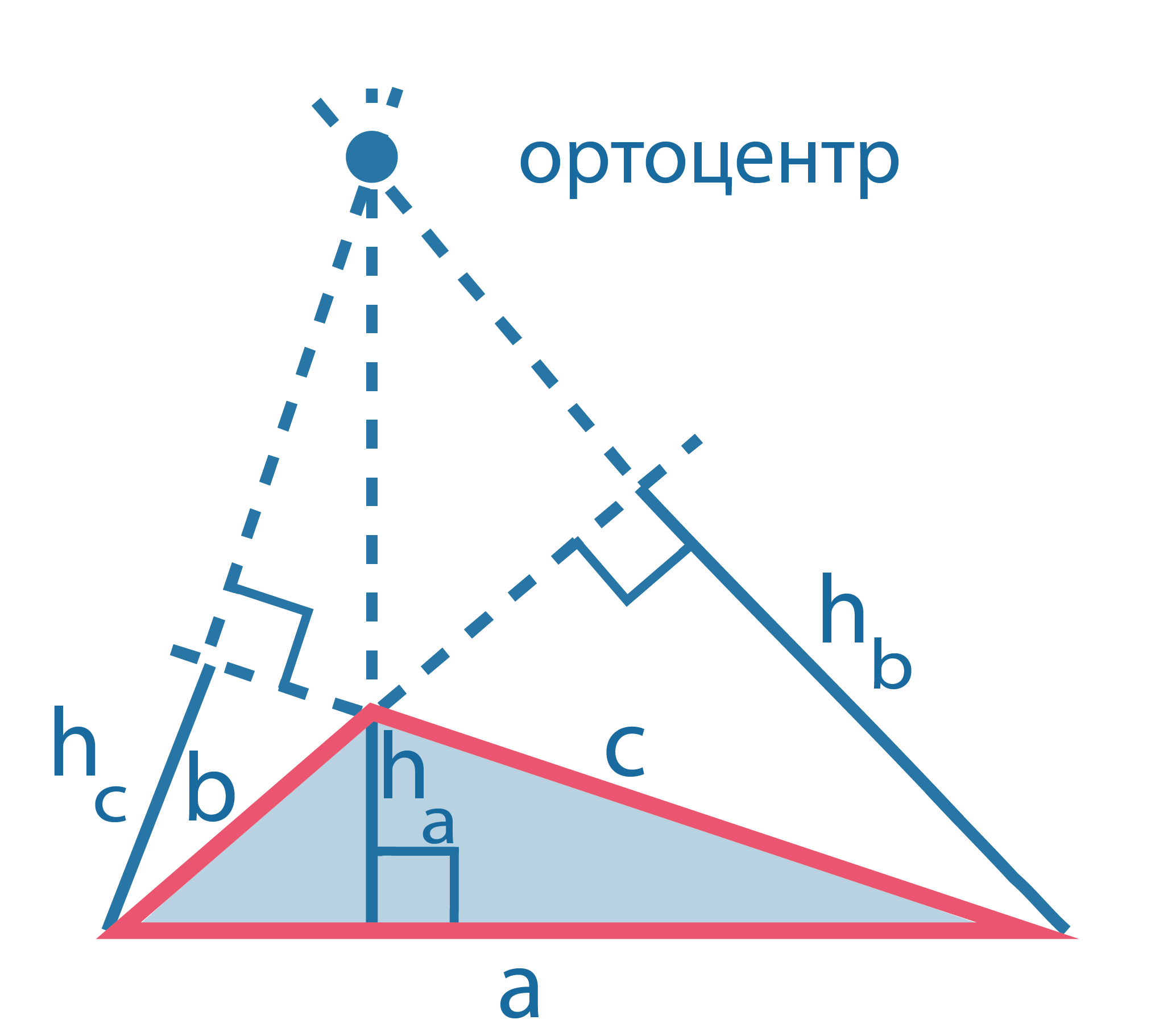 |
Ортоцентр тупоугольного треугольника лежит вне треугольника (продолжения высот и сторон, образующих тупой угол, проведены пунктиром). |
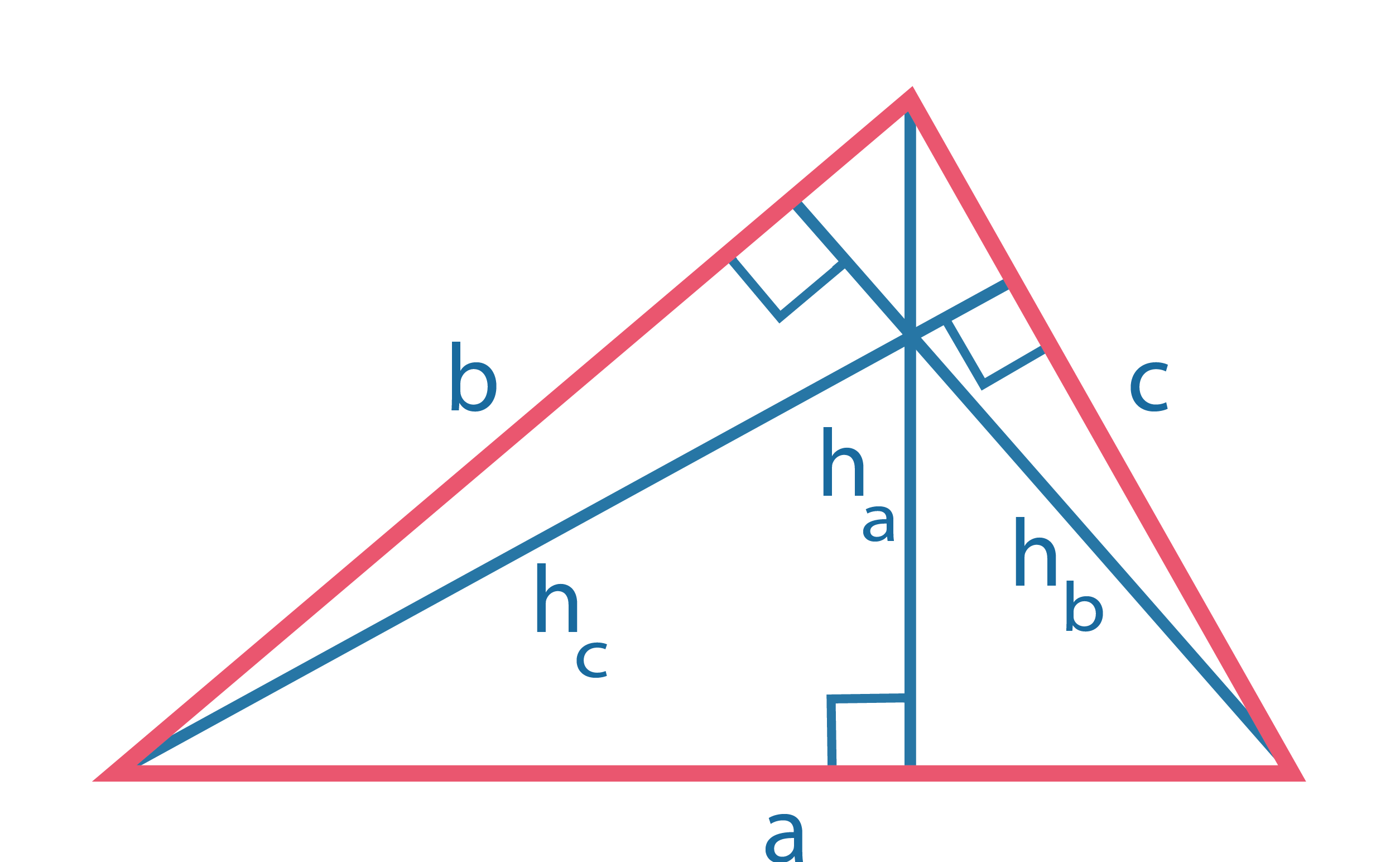 |
Высоты треугольника обратно пропорциональны его сторонам: \(h_a:h_b:h_c={1 \over a}:{1 \over b}: {1 \over c}\) |
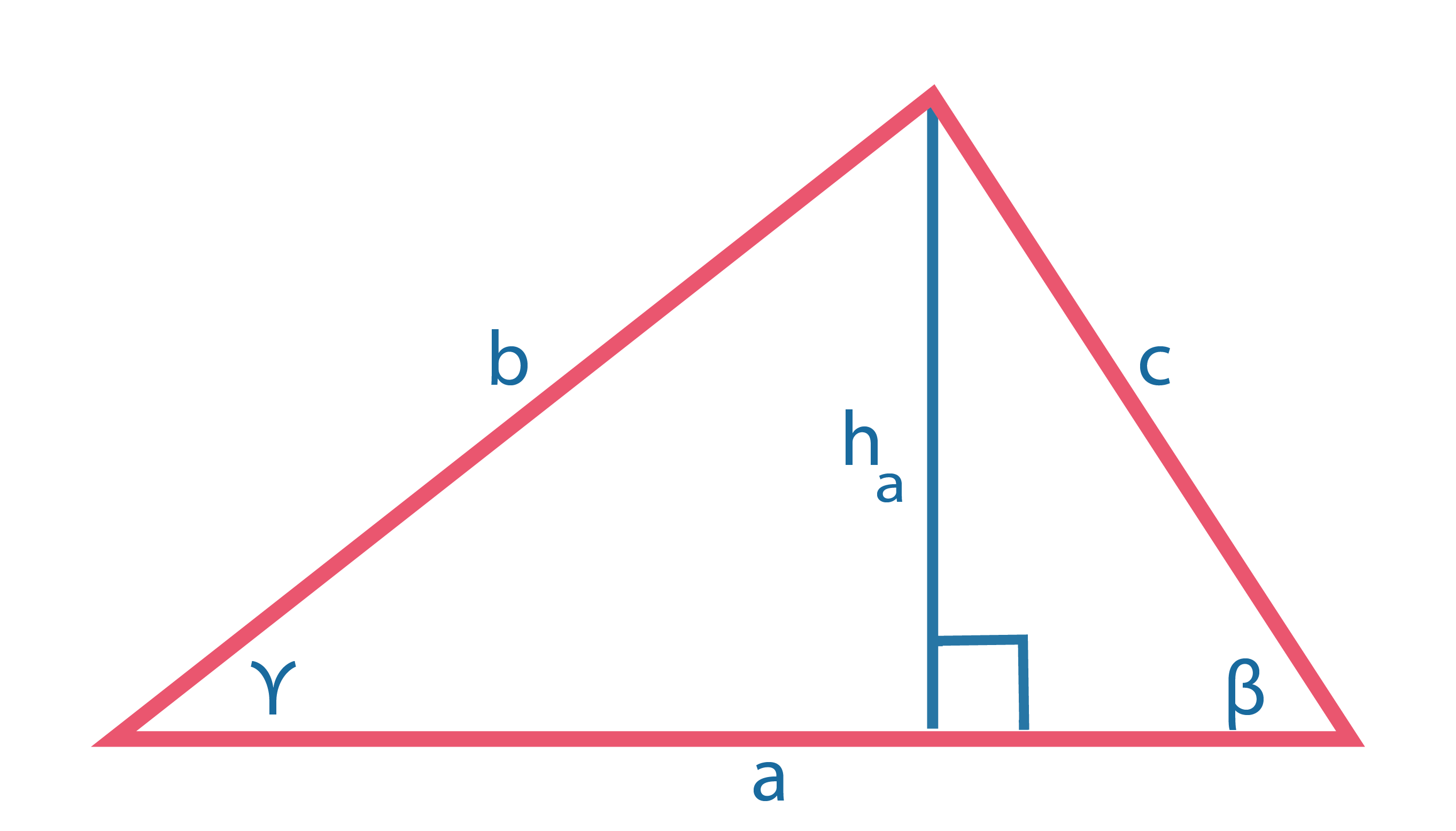 |
Длина высоты: \(h_a=b~sin~\gamma=c~sin~\beta\) \(h_a={2S \over a}={2 \sqrt{p(p-a)(p-b)(p-c)} \over a}\), где \(p={a+b+c \over 2}\) |
Свойства средней линии
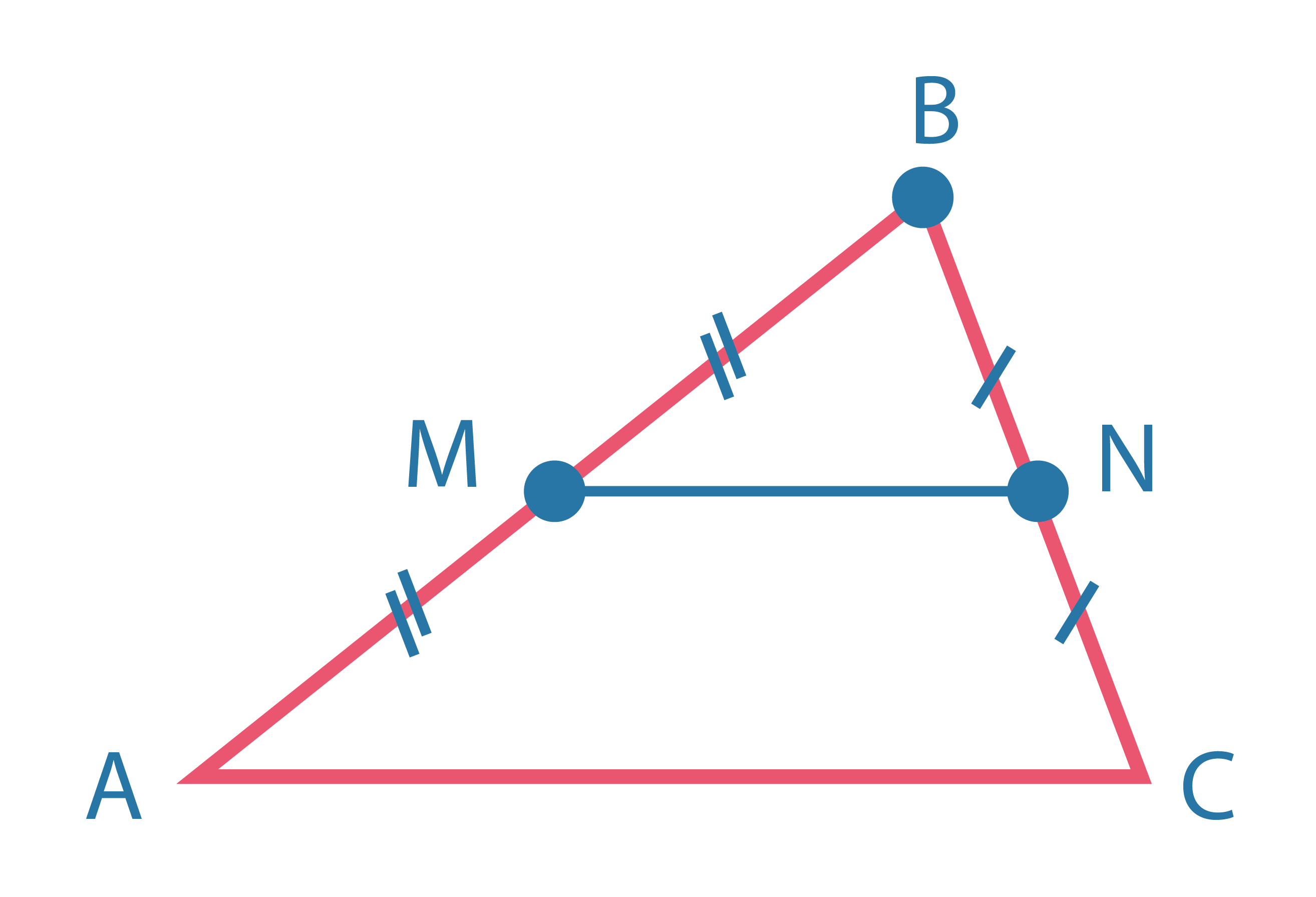 |
Средняя линия параллельна одной из сторон треугольника и равна её половине: \(MN \parallel AC;~ MN={1\over 2}AC\) Она отсекает треугольник, подобный данному, с коэффициентом подобия \(1/2\) |
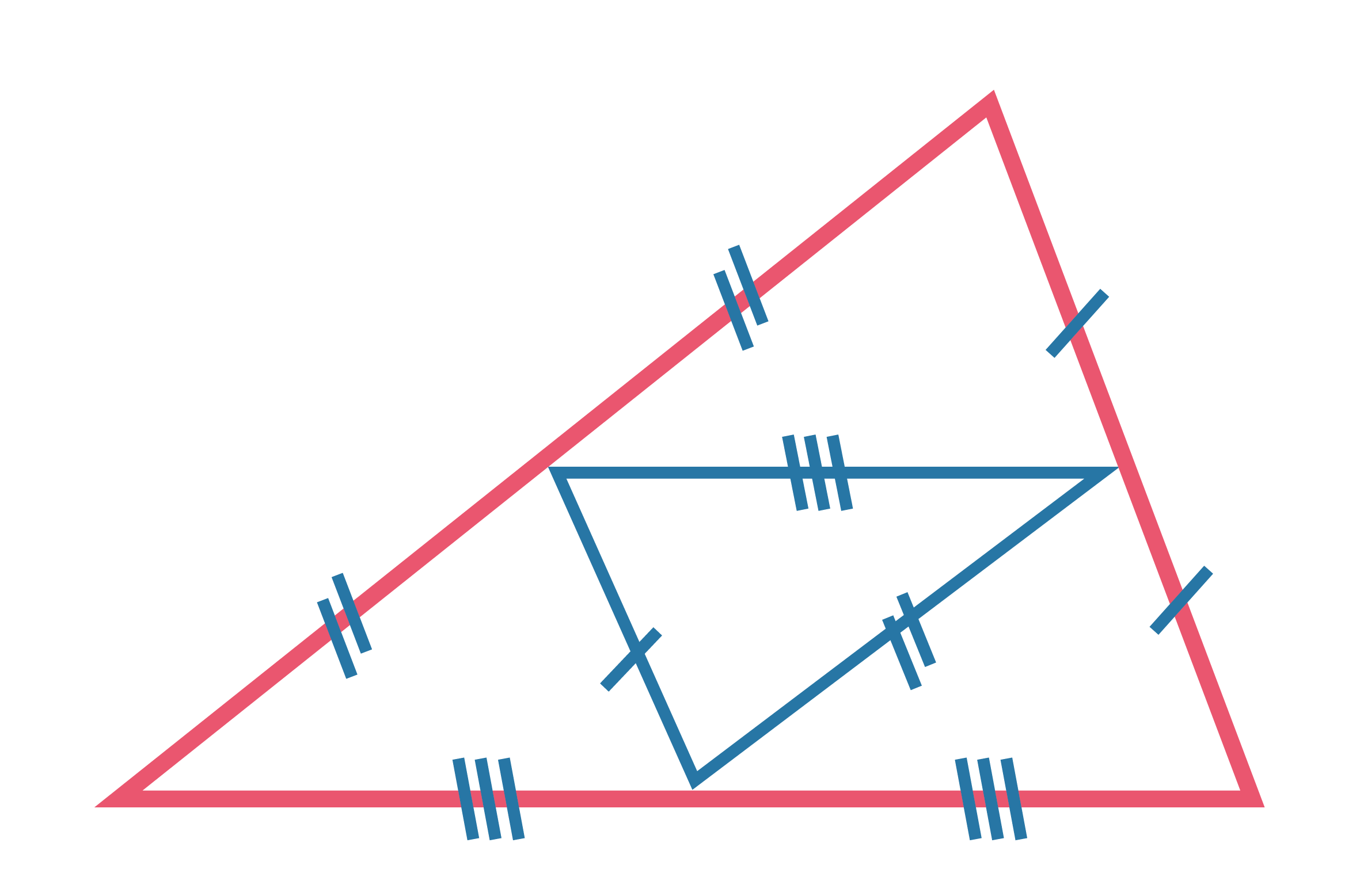 |
Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия \(1/2\). |
Площадь треугольника
|
|
Через сторону и высоту, проведенную к ней: \(S={1 \over2}ah_a\) |
|
|
Через две стороны и угол между ними: \(S={1 \over2}ab ~sin \gamma\) |
|
|
Формула Герона Через три стороны: \(S= \sqrt {p(p-a)(p-b)(p-c)}\), |
|
|
Через полупериметр и радиус вписанной окружности: \(S=pr\), |
|
|
Через произведение сторон и радиус описанной окружности: \(S={abc\over4R}\) |
Площадь прямоугольного треугольника
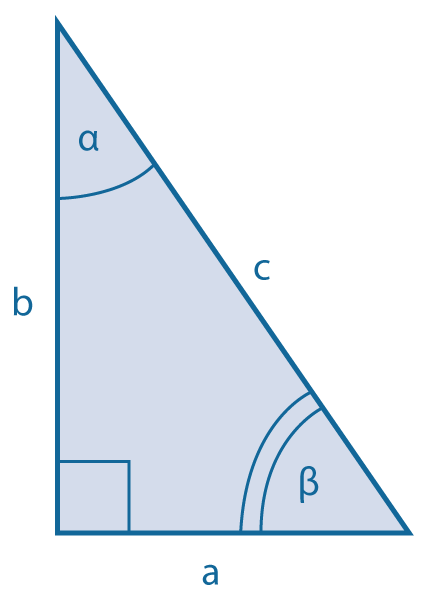 |
Через катеты: \(S={1\over2}ab\) Через катет и острый угол: Через гипотенузу и любой из острых углов: |