
Ленинский пр-т, 32а
| Основное тригонометрическое тождество | ||
| \(sin^2\alpha+cos^2\alpha=1\) | \(tg^2\alpha+1={1\over cos^2\alpha}\) | \(1+ctg^2\alpha={ 1\over sin^2\alpha }\) |
| Формулы сложения | |
|
\(sin(\alpha \ + \ \beta)=sin\alpha \cdot cos\beta \ + \ cos\alpha \cdot sin\beta\) \(sin(\alpha \ - \ \beta)=sin\alpha \cdot cos\beta \ - \ cos\alpha \cdot sin\beta\) |
\(tg(\alpha \ + \ \beta) = {{tg\alpha \ + \ tg\beta} \over {1 \ - \ tg\alpha\cdot tg\beta} }\) \(tg(\alpha \ - \ \beta) = {{tg\alpha \ - \ tg\beta} \over {1 \ + \ tg\alpha\cdot tg\beta} }\) |
|
\(cos(\alpha \ + \ \beta)=cos\alpha \cdot cos\beta \ - \ sin\alpha \cdot sin\beta\) \(cos(\alpha \ - \ \beta)=cos\alpha \cdot cos\beta \ + \ sin\alpha \cdot sin\beta\) |
\(ctg(\alpha \ + \ \beta) = {{ctg\alpha \cdot ctg\beta \ - \ 1} \over {ctg\alpha \ + \ ctg\beta} }\) \(ctg(\alpha \ - \ \beta) = {{ctg\alpha \cdot ctg\beta \ + \ 1} \over {ctg\beta \ - \ ctg\alpha} }\) |
| Формулы двойного угла | Формулы тройного угла | ||
| \(sin2\alpha=2sin\alpha \cdot cos\alpha\) | \(tg2\alpha={2tg\alpha \over 1-tg^2\alpha}\) | \(sin3\alpha=3sin\alpha - 4sin^3\alpha\) | \(tg3\alpha={3tg\alpha - tg^3\alpha \over 1-3tg^2\alpha}\) |
|
\(cos2\alpha=cos^2\alpha-sin^2\alpha\) \(cos2\alpha=2cos^2\alpha-1\) \(cos2\alpha=1-2sin^2\alpha\) |
\(ctg2\alpha={ctg^2\alpha-1 \over 2ctg\alpha}\) | \(cos3\alpha=4cos^3\alpha-3cos\alpha\) | |
| Формулы понижения степени | Формулы тангенса половинного угла | Универсальная подстановка |
|
\(cos^2\alpha = {1 \ + \ cos2\alpha \over 2}\) \(sin^2\alpha = {1 \ - \ cos2\alpha \over 2}\) |
\(tg^2{\alpha \over 2} = {1 \ - \ cos\alpha \over 1 \ + \ cos\alpha}\) \(tg{\alpha \over 2} = {1 \ - \ cos\alpha \over \ sin\alpha}\) \(tg{\alpha \over 2} = {sin\alpha \over 1 \ + \ cos\alpha}\) |
\(sin\alpha = {2tg{\alpha \over 2} \over {1 \ + \ tg^2{\alpha \over 2}}}\) \(cos\alpha = {1 \ - \ tg^2{\alpha \over 2} \over {1 \ + \ tg^2{\alpha \over 2}}}\) \(tg\alpha = {2tg{\alpha \over 2} \over {1 \ - \ tg^2{\alpha \over 2}}}\) \(ctg\alpha = {1 \ - \ tg^2{\alpha \over 2} \over {2tg{\alpha \over 2}}}\) |
| Суммы и произведения тригонометрических функций | |
|
\(sin\alpha \ + \ sin\beta=2sin{\alpha + \beta \over 2}\cdot cos{\alpha - \beta \over 2}\) \(sin\alpha \ - \ sin\beta=2sin{\alpha - \beta \over 2}\cdot cos{\alpha + \beta \over 2}\) \(cos\alpha \ + \ cos\beta=2cos{\alpha + \beta \over 2}\cdot cos{\alpha - \beta \over 2}\) \(cos\alpha \ - \ cos\beta=2sin{\alpha + \beta \over 2}\cdot sin{\alpha - \beta \over 2}\) \(2cos\alpha\cdot cos\beta = cos(\alpha \ + \ \beta) \ + \ cos(\alpha \ - \ \beta)\) \(2sin\alpha\cdot sin\beta = cos(\alpha \ - \ \beta) \ - \ cos(\alpha \ + \ \beta)\) \(2sin\alpha\cdot cos\beta = sin(\alpha \ + \ \beta) \ + \ sin(\alpha \ - \ \beta)\) |
\(tg\alpha \ + \ tg\beta = {sin(\alpha \ + \ \beta)\over cos\alpha\cdot cos\beta}\) \(tg\alpha \ - \ tg\beta = {sin(\alpha \ - \ \beta)\over cos\alpha\cdot cos\beta}\) \(ctg\alpha \ + \ ctg\beta = {sin(\alpha \ + \ \beta)\over sin\alpha\cdot sin\beta}\) \(ctg\alpha \ - \ ctg\beta = {sin(\beta \ - \ \alpha)\over sin\alpha\cdot sin\beta}\) \(tg\alpha \ + \ ctg\beta = {cos(\alpha \ - \ \beta)\over cos\alpha\cdot sin\beta}\) \(ctg\alpha \ - \ tg\beta = {cos(\alpha \ + \ \beta)\over sin\alpha\cdot cos\beta}\) |
| Тригонометрические функции | ||
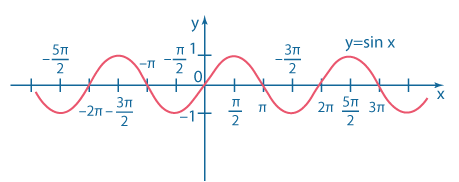
| \(y=\sin x\) |
\(D(y)=(-\infty; +\infty) \\ E(y) = [-1;1]\) |
 |
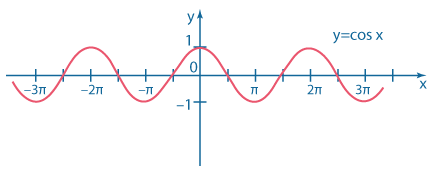
| \(y=\cos x\) | \(D(y)=(-\infty; +\infty) \\ E(y) = [-1;1]\) Период \(T=2\pi.\) Четная функция. |
 |
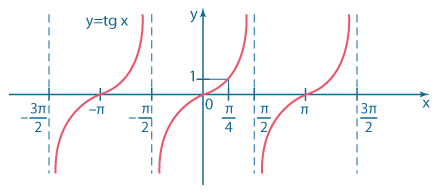
| \(y=tg \ x\) | \(D(y)=(-{\pi\over 2} + \pi k; {{\pi \over 2} + \pi k}) \\ E(y) = (-\infty;+\infty)\) Период \(T=\pi.\) Нечетная функция. Возрастает на всей области определения. Асимптоты \(x={\pi \over 2} + \pi k.\) |
 |
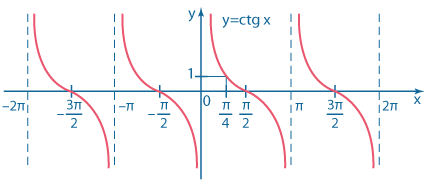
| \(y=ctg \ x\) | \(D(y)=(\pi k; \ {2\pi k}) \\ E(y) = (-\infty;+\infty)\) Период \(T=\pi.\) Убывает на всей области определния. Асимптоты \(x= \pi k.\) |
 |