Параллелограмм
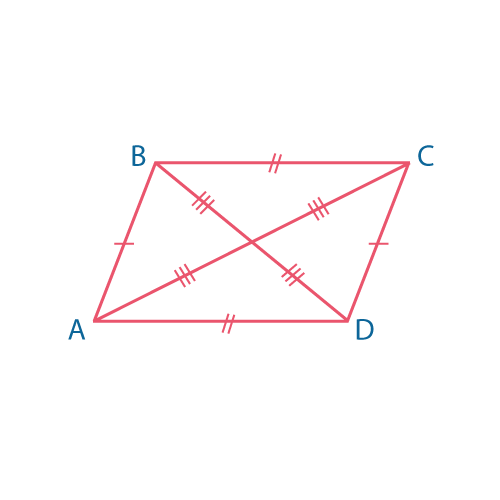
\(AB || CD, \quad BC||AD\)
Параллелограмм — это четырёхугольник, у которого две пары противоположных сторон параллельны.
Свойства параллелограмма:
- У параллелограмма противолежащие углы равны.
- У параллелограмма противолежащие стороны равны.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Признаки параллелограмма:
- Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
- Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
- Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Биссектриса в параллелограмме
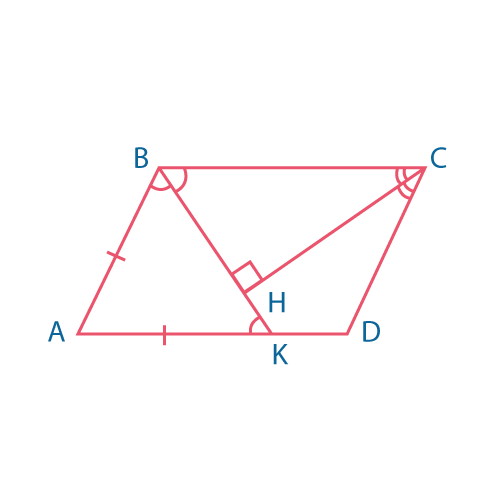
- Биссектрисы углов, прилежащих одной стороне, перпендикулярны.
- Биссектриса отсекает равнобедренный треугольник.
Прямоугольник
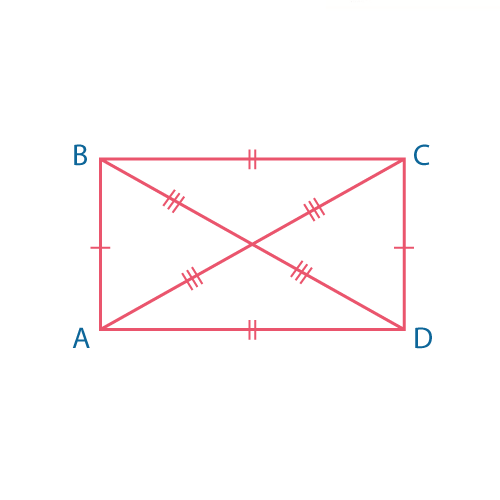
Прямоугольник — это параллелограмм, у которого все углы прямые.
Дополнительные свойства прямоугольника:
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Диагонали равны.
Признаки прямоугольника.
- Если в четырёхугольнике \(3\) угла — прямые, то такой четырёхугольник — прямоугольник.
- Если в параллелограмме \(1\) угол прямой, то такой параллелограмм — прямоугольник.
- Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромб
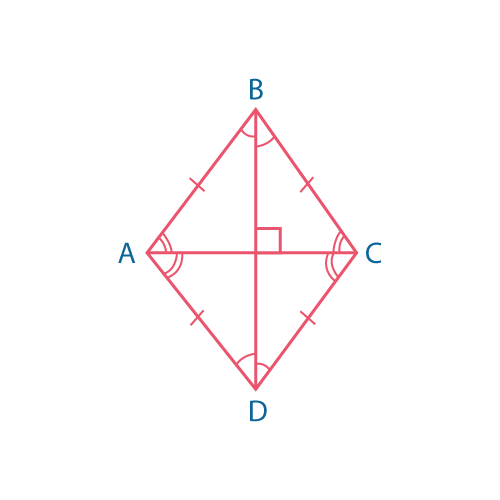
\(AB=BC=CD=AD\)
Ромб — это параллелограмм с равными сторонами.
Дополнительные свойства ромба:
- Диагонали ромба перпендикулярны.
- Диагонали ромба делят его углы пополам.
Признаки ромба:
- Четырёхугольник, у которого все стороны равны, является ромбом.
- Параллелограмм, у которого диагонали взаимно перпендикулярны является ромбом.
- Параллелограмм, у которого диагонали являются биссектрисами углов, является ромбом.
- Параллелограмм, у которого две смежные стороны равны, является ромбом.
Квадрат
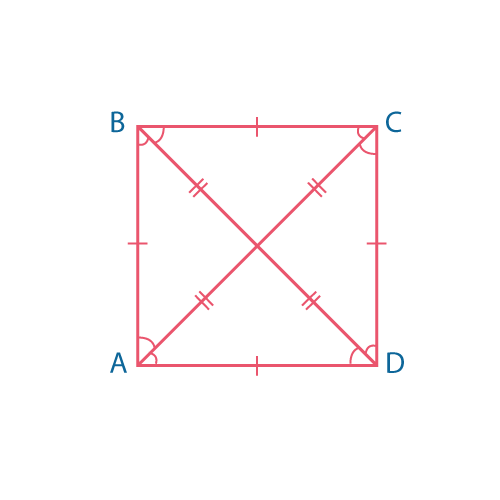
\(AB\perp AD, \quad AB=BC=CD=AD\)
Квадрат — параллелограмм, у которого все углы прямые и все стороны равны.
Свойства квадрата — все свойства ромба и прямоугольника.
Признаки квадата:
- Четырехугольник является квадратом, если все стороны равны и среди внутренних углов есть прямой угол.
- Четырехугольник является квадратом, если его диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
Трапеция
Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
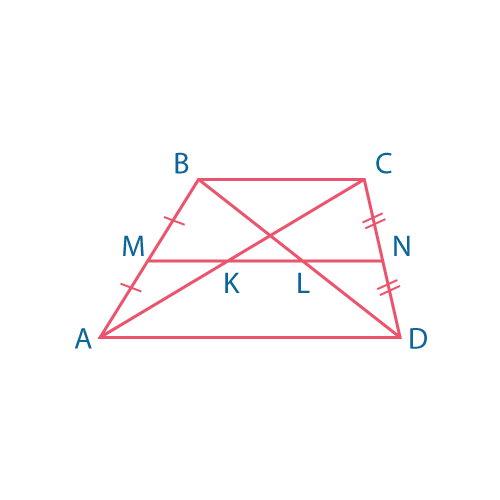
\(MN||BC||AD\)
\(MN={1\over 2}(BC + AD)\)
Средняя линия трапеции соединяет середины боковых сторон.
Свойства средней линии:
- Параллельна основаниям.
- Равна полусумме оснований.
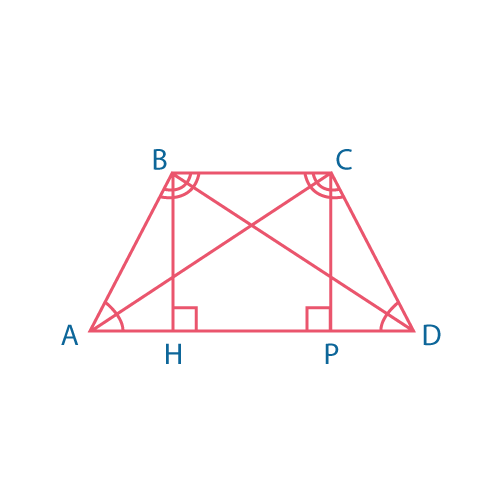
\(AB=CD\)
\(AC=BD\)
\(AH=PD\)
Равнобокая (равнобедренная) трапеция – трапеция с равными боковыми сторонами.
Свойства равнобокой трапеции:
- Углы при каждом из её оснований равны.
- Диагонали равны.
- Проекции боковых сторон на большее основание равны.
Признаки равнобокой трапеции:
- Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной.
- Если у трапеции диагонали равны, то она является равнобедренной.
Дельтоид
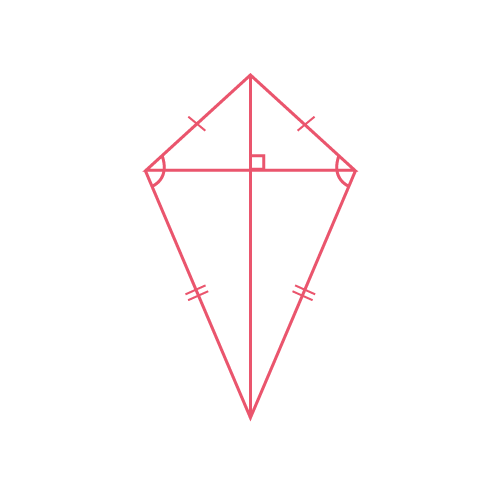
Дельтоид – это четырёхугольник, у которого смежные стороны попарно равны.
Свойства дельтоида:
- Диагонали перпендикулярны.
- Углы, образованные парами неравных сторон, равны.
Площади четырёхугольников
|
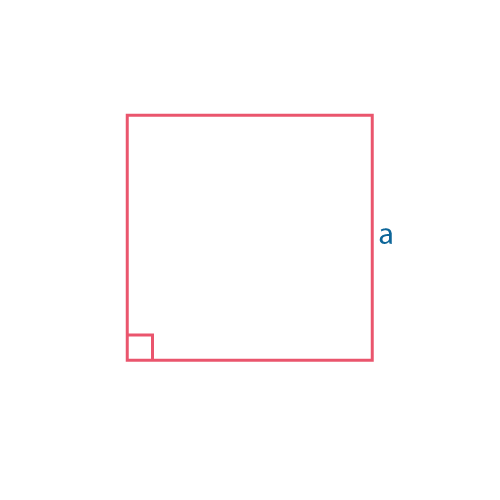
Квадрат
|
\(S=a^2\) |
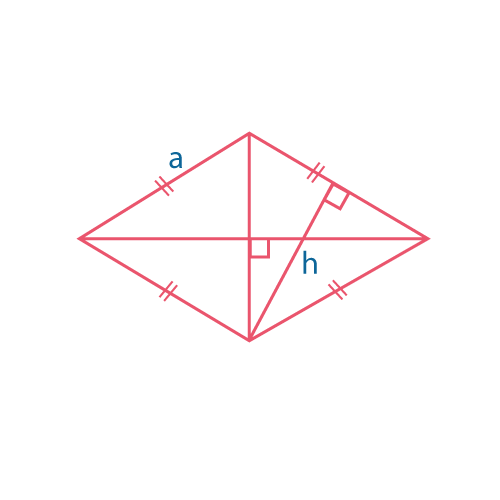
Ромб
|
\(S=ah={d_1d_2\over 2}\)
\(d_1,d_2\) – диагонали.
|
|
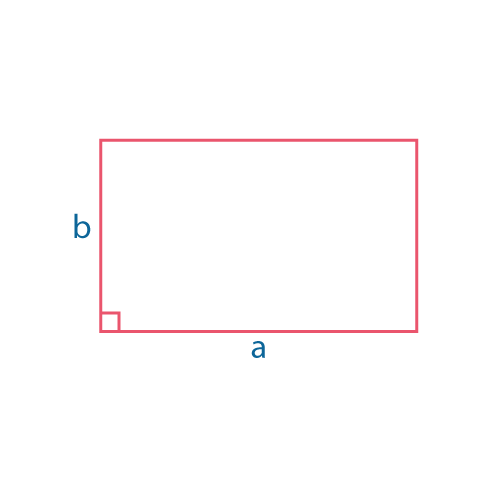
Прямоугольник
|
\(S=ab\) |
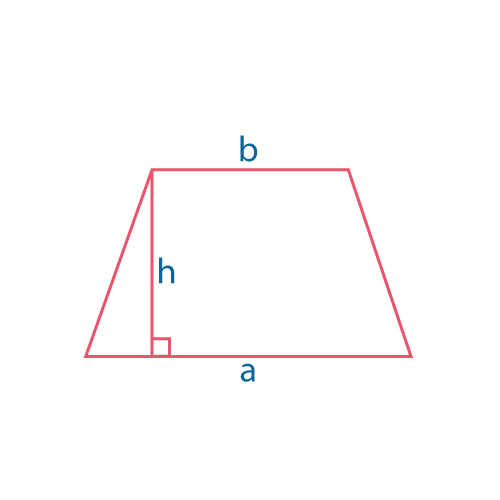
Трапеция
|
\(S={{a+b}\over 2}h\) |
|
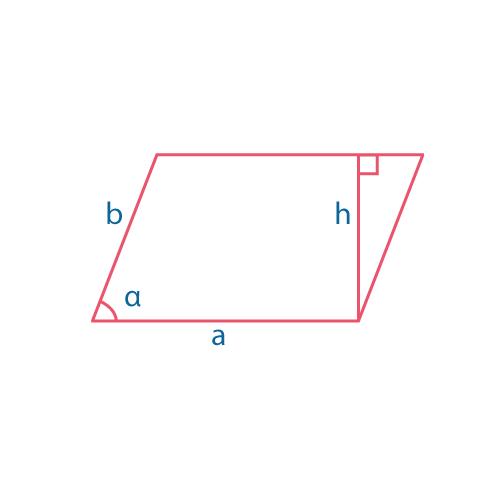
Параллелограмм
|
\(S=ah=absin\alpha\)
\(h\) – высота
|
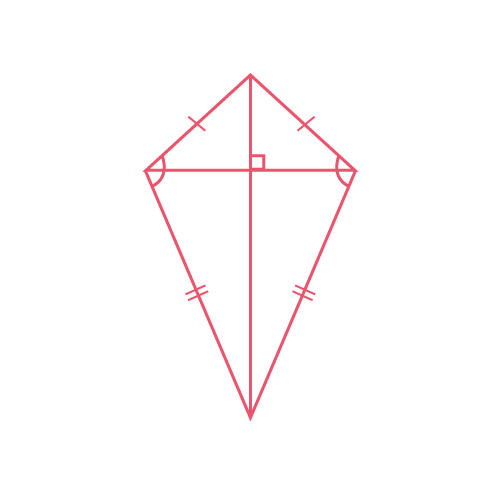
Дельтоид
|
\(S={d_1d_2\over 2}\) |
Сечения многогранников
Пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Отрезки образуют некий плоский многоугольник, который мы называем сечением.
Этапы построения сечения по определению:
- соединяем точки сечения, принадлежащие одной грани;
- пересекаем прямые, такие, что:
- одна лежит в плоскости сечения, а другая лежит в плоскости грани, в которой мы хотим получить отрезок сечения;
- обе прямые точно лежат в одной плоскости (указываем явно, в какой плоскости они лежат);
- полученную точку пересечения соединяем с другой точкой сечения в плоскости той же грани;
- находим точки пересечения с рёбрами многогранника;
- соединяем их, получаем отрезок сечения.
Пример:
построить сечение правильной треугольной призмы по указанным точкам.
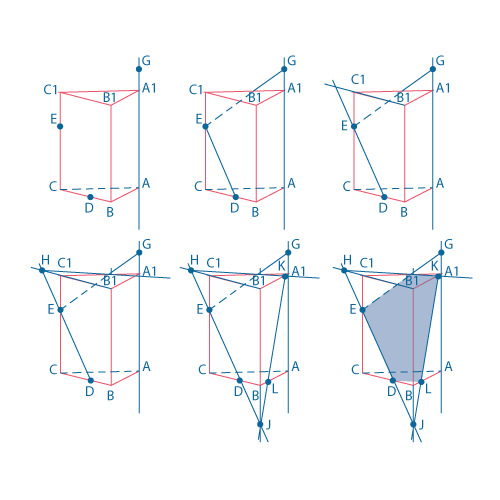
Применение свойства параллельных плоскостей
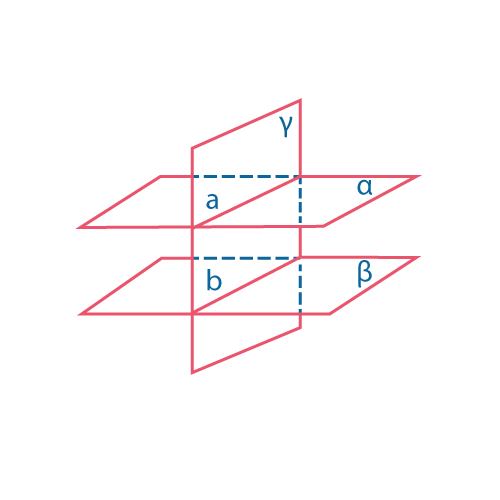
Свойство параллельных плоскостей:
если две параллельные плоскости пересекаются третьей, то линии пересечения параллельны.










